AT_abc406_f [ABC406F] Compare Tree Weights

$ N $ 頂点の木 $ T $ があり、 頂点および辺はそれぞれ頂点 $ 1 $ , 頂点 $ 2 $ , $ \ldots $ , 頂点 $ N $ 、辺 $ 1 $ , 辺 $ 2 $ , $ \ldots $ , 辺 $ (N-1) $ と番号づけられています。 特に、辺 $ i $ $ (1\leq i\leq N-1) $ は頂点 $ U_i $ と頂点 $ V_i $ を結んでいます。 また、各頂点には重みが定められており、最初、各頂点の重みはすべて $ 1 $ です。 $ Q $ 個のクエリが与えられるので、順に処理してください。 各クエリは次の $ 2 $ 種類のいずれかです。 - `1 x w` : 頂点 $ x $ の重みを $ w $ 増加させる。 - `2 y` : 辺 $ y $ を削除すると、 $ T $ は $ 2 $ つの部分木（連結成分）に分かれる。それぞれの部分木に含まれる頂点の重みの総和をその部分木の重みとするとき、 $ 2 $ つの部分木の重みの差を出力する。 $ 2 $ 種類目のクエリについて、 $ T $ から任意の辺を $ 1 $ つ選んで削除したとき、 $ T $ は必ず $ 2 $ つの部分木に分かれることが証明できます。 また、 $ 2 $ 種類目のクエリでは、実際に辺を削除しているわけではないことに注意してください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ U_1 $ $ V_1 $ $ U_2 $ $ V_2 $ $ \vdots $ $ U_{N-1} $ $ V_{N-1} $ $ Q $ $ \mathrm{query}_1 $ $ \mathrm{query}_2 $ $ \vdots $ $ \mathrm{query}_Q $ 各クエリ $ \mathrm{query}_i $ $ (1\leq i\leq Q) $ は次の形式のいずれかで与えられる。 > $ 1 $ $ x $ $ w $ > $ 2 $ $ y $

$ 2 $ 種類目のクエリの個数を $ K $ 個として、 $ K $ 行出力せよ。 $ i $ 行目 $ (1\leq i\leq K) $ には $ i $ 番目の $ 2 $ 種類目のクエリに対する答えを出力せよ。

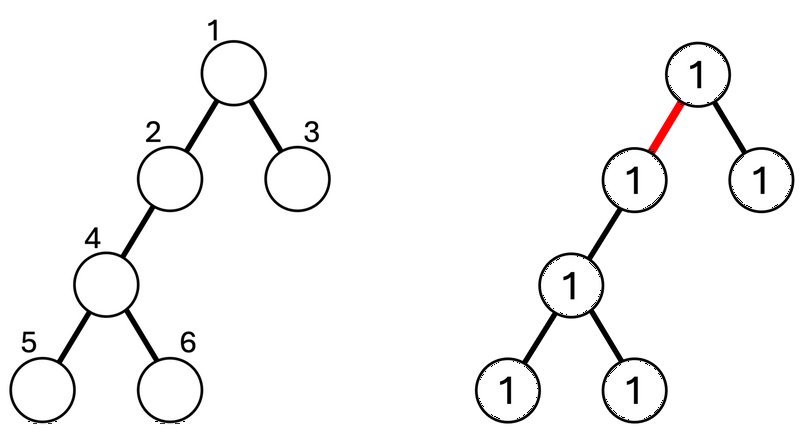
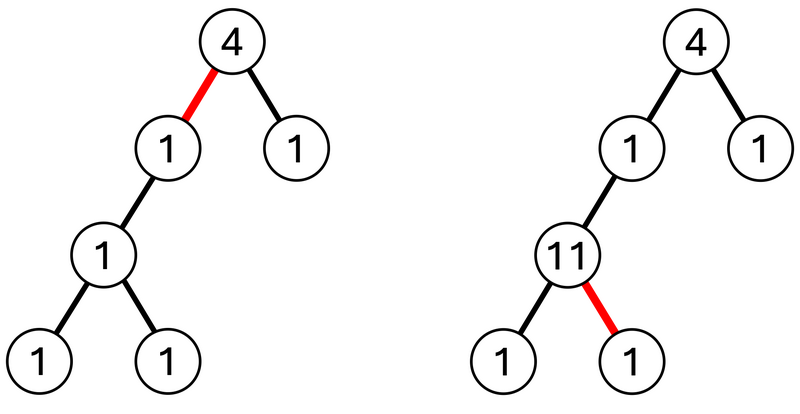
### Sample Explanation 1 木 $ T $ の構造、頂点番号の対応は下図左の通りです。最初、各頂点の重みはすべて $ 1 $ です。 $ 1 $ 番目のクエリでは、辺 $ 1 $ を削除することを考えます。 このとき、頂点 $ 1 $ を含む部分木と頂点 $ 2 $ を含む部分木に分かれます。 頂点 $ 1 $ を含む部分木の重みは $ 2 $ 、頂点 $ 2 $ を含む部分木の重みは $ 4 $ であるため、その差の $ 2 $ を出力します。（下図右）  $ 2 $ 番目のクエリでは、頂点 $ 1 $ の重みを $ 3 $ 増加させます。 $ 3 $ 番目のクエリでは、辺 $ 1 $ を削除することを考えます。 頂点 $ 1 $ を含む部分木の重みは $ 5 $ 、頂点 $ 2 $ を含む部分木の重みは $ 4 $ であるため、その差の $ 1 $ を出力します。（下図左） $ 4 $ 番目のクエリでは、頂点 $ 4 $ の重みを $ 10 $ 増加させます。 $ 5 $ 番目のクエリでは、辺 $ 5 $ を削除することを考えます。 このとき、頂点 $ 4 $ を含む部分木と頂点 $ 6 $ のみからなる部分木に分かれます。 頂点 $ 4 $ を含む部分木の重みは $ 18 $ 、頂点 $ 6 $ のみからなる部分木の重みは $ 1 $ であるため、その差の $ 17 $ を出力します。（下図右）  よって、 $ 2 $ 種類目のクエリの答えである $ 2,1,17 $ をこの順に改行区切りで出力します。 ### Constraints - $ 2\leq N\leq 3\times 10^5 $ - $ 1\leq U_i,V_i\leq N $ - $ 1\leq Q\leq 3\times 10^5 $ - $ 1\leq x\leq N $ - $ 1\leq w\leq 1000 $ - $ 1\leq y\leq N-1 $ - 入力はすべて整数 - 与えられるグラフは木である。 - $ 2 $ 種類目のクエリが少なくとも $ 1 $ つ存在する。