AT_abc407_d [ABC407D] Domino Covering XOR

$ H $ 行 $ W $ 列のマス目があります。 上から $ i $ 行目 $ (1\leq i\leq H) $ 、左から $ j $ 列目 $ (1\leq j\leq W) $ のマスをマス $ (i,j) $ と呼ぶことにします。 マス $ (i,j)\ (1\leq i\leq H,1\leq j\leq W) $ には非負整数 $ A _ {i,j} $ が書かれています。 このマス目にドミノを $ 0 $ 個以上置きます。 $ 1 $ つのドミノは隣り合う $ 2 $ つのマス、つまり - $ 1\leq i\leq H,1\leq j\lt W $ に対するマス $ (i,j) $ とマス $ (i,j+1) $ - $ 1\leq i\lt H,1\leq j\leq W $ に対するマス $ (i,j) $ とマス $ (i+1,j) $ のどれかに置くことができます。 ただし、同じマスに対して複数のドミノを置くことはできません。 ドミノの置き方に対して、置き方の**スコア**をドミノが**置かれていない**マスに書かれた整数すべてのビットごとの排他的論理和として定めます。 ドミノの置き方のスコアとしてありうる最大値を求めてください。 ビットごとの排他的論理和とは 非負整数 $ A, B $ のビットごとの排他的論理和 $ A \oplus B $ は、以下のように定義されます。 - $ A \oplus B $ を二進表記した際の $ 2^k $ ( $ k \geq 0 $ ) の位の数は、 $ A, B $ を二進表記した際の $ 2^k $ の位の数のうち一方のみが $ 1 $ であれば $ 1 $ 、そうでなければ $ 0 $ である。 例えば、 $ 3 \oplus 5 = 6 $ となります (二進表記すると: $ 011 \oplus 101 = 110 $ )。 一般に $ k $ 個の非負整数 $ p_1, p_2, p_3, \dots, p_k $ のビット単位 $ \mathrm{XOR} $ は $ (\dots ((p_1 \oplus p_2) \oplus p_3) \oplus \dots \oplus p_k) $ と定義され、これは $ p_1, p_2, p_3, \dots, p_k $ の順番によらないことが証明できます。

入力は以下の形式で標準入力から与えられる。 > $ H $ $ W $ $ A _ {1,1} $ $ A _ {1,2} $ $ \ldots $ $ A _ {1,W} $ $ A _ {2,1} $ $ A _ {2,2} $ $ \ldots $ $ A _ {2,W} $ $ \vdots $ $ A _ {H,1} $ $ A _ {H,2} $ $ \ldots $ $ A _ {H,W} $

答えを出力せよ。

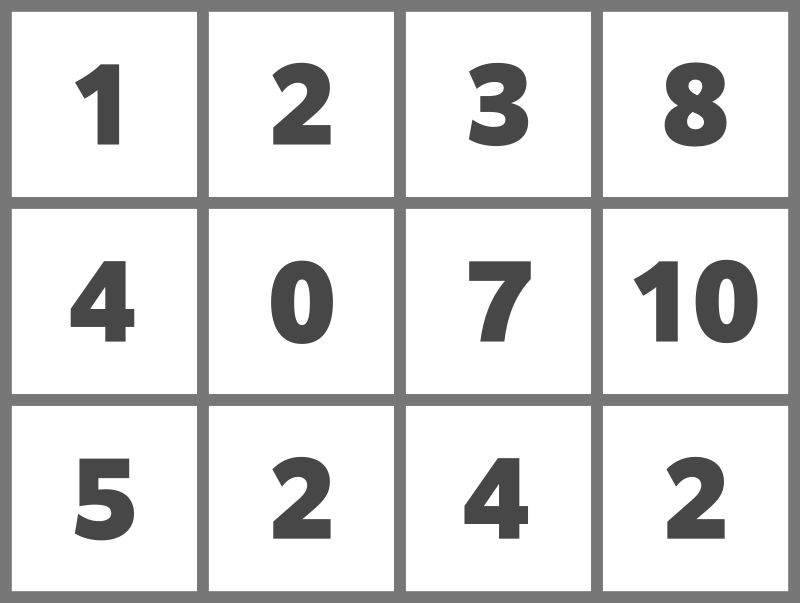
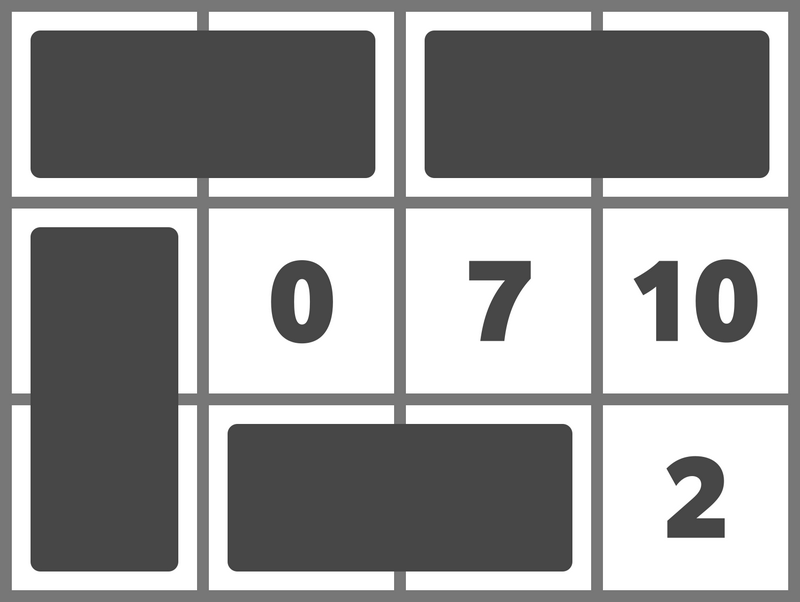
### Sample Explanation 1 与えられたマス目は以下のようになります。  例えば、次のようにドミノを置くことでスコアを $ 15 $ とすることができます。  スコアを $ 16 $ 以上にすることはできないため、`15` を出力してください。 ### Sample Explanation 2 ドミノを $ 1 $ 枚も置かないこともできます。 ### Constraints - $ 1\leq H $ - $ 1\leq W $ - $ HW\leq20 $ - $ 0\leq A _ {i,j}\lt 2 ^ {60}\ (1\leq i\leq H,1\leq j\leq W) $ - 入力はすべて整数