AT_abc407_g [ABC407G] Domino Covering SUM

There is a grid with $ H $ rows and $ W $ columns. Let $ (i,j) $ denote the cell at the $ i $ -th row from the top $ (1\leq i\leq H) $ and the $ j $ -th column from the left $ (1\leq j\leq W) $ . Cell $ (i,j)\ (1\leq i\leq H,1\leq j\leq W) $ has an integer $ A_{i,j} $ written on it. Let us place zero or more dominoes on the grid. A domino covers two adjacent cells, namely one of the following pairs: - cells $ (i,j) $ and $ (i,j+1) $ for $ 1\leq i\leq H,1\leq j\lt W $ ; - cells $ (i,j) $ and $ (i+1,j) $ for $ 1\leq i\lt H,1\leq j\leq W $ . No cell may be covered by more than one domino. For a placement of dominoes, define its **score** as the sum of all integers written in cells **not** covered by any domino. Find the maximum possible score.

The input is given from Standard Input in the following format: > $ H $ $ W $ $ A _ {1,1} $ $ A _ {1,2} $ $ \ldots $ $ A _ {1,W} $ $ A _ {2,1} $ $ A _ {2,2} $ $ \ldots $ $ A _ {2,W} $ $ \vdots $ $ A _ {H,1} $ $ A _ {H,2} $ $ \ldots $ $ A _ {H,W} $

Output the answer.

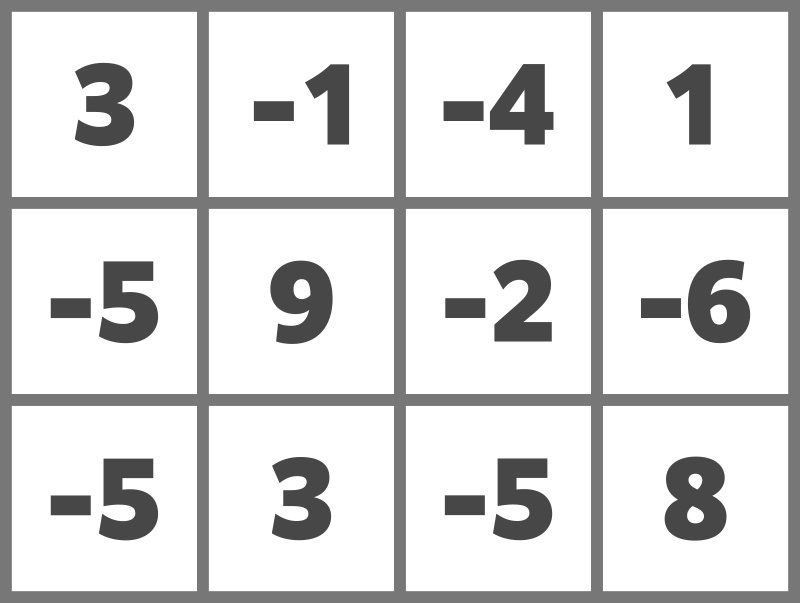
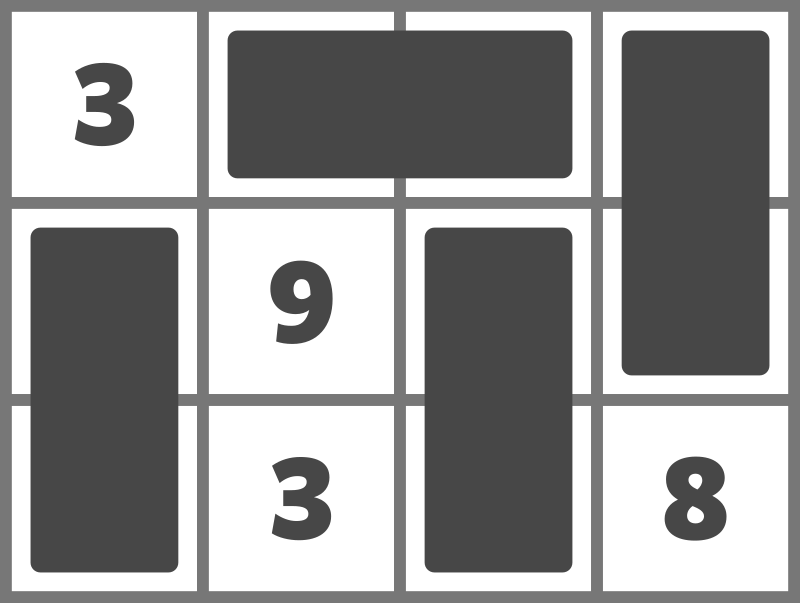
### Sample Explanation 1 The grid is as follows:  For example, the placement below yields a score of $ 23 $ .  No placement achieves a score of $ 24 $ or higher, so output `23`. ### Constraints - $ 1\leq H $ - $ 1\leq W $ - $ HW\leq2000 $ - $ -10 ^ {12}\leq A _ {i,j}\leq10 ^ {12}\ (1\leq i\leq H,1\leq j\leq W) $ - All input values are integers.