AT_abc407_g [ABC407G] Domino Covering SUM

$ H $ 行 $ W $ 列のマス目があります。 上から $ i $ 行目 $ (1\leq i\leq H) $ 、左から $ j $ 列目 $ (1\leq j\leq W) $ のマスをマス $ (i,j) $ と呼ぶことにします。 マス $ (i,j)\ (1\leq i\leq H,1\leq j\leq W) $ には整数 $ A _ {i,j} $ が書かれています。 このマス目にドミノを $ 0 $ 個以上置きます。 $ 1 $ つのドミノは隣り合う $ 2 $ つのマス、つまり - $ 1\leq i\leq H,1\leq j\lt W $ に対するマス $ (i,j) $ とマス $ (i,j+1) $ - $ 1\leq i\lt H,1\leq j\leq W $ に対するマス $ (i,j) $ とマス $ (i+1,j) $ のどれかに置くことができます。 ただし、同じマスに対して複数のドミノを置くことはできません。 ドミノの置き方に対して、置き方の**スコア**をドミノが**置かれていない**マスに書かれた整数すべての和として定めます。 ドミノの置き方のスコアとしてありうる最大値を求めてください。

入力は以下の形式で標準入力から与えられる。 > $ H $ $ W $ $ A _ {1,1} $ $ A _ {1,2} $ $ \ldots $ $ A _ {1,W} $ $ A _ {2,1} $ $ A _ {2,2} $ $ \ldots $ $ A _ {2,W} $ $ \vdots $ $ A _ {H,1} $ $ A _ {H,2} $ $ \ldots $ $ A _ {H,W} $

答えを出力せよ。

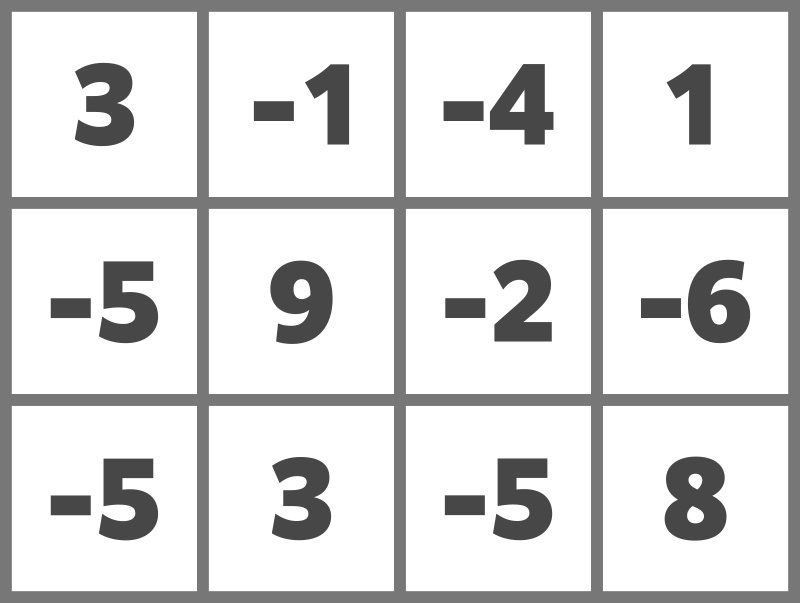
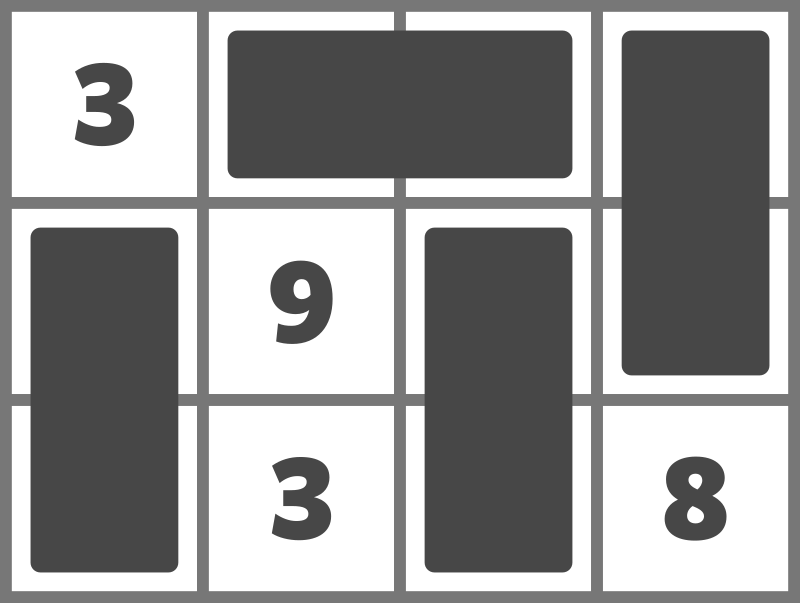
### Sample Explanation 1 与えられたマス目は以下のようになります。  例えば、次のようにドミノを置くことでスコアを $ 23 $ とすることができます。  スコアを $ 24 $ 以上にすることはできないため、`23` を出力してください。 ### Constraints - $ 1\leq H $ - $ 1\leq W $ - $ HW\leq2000 $ - $ -10 ^ {12}\leq A _ {i,j}\leq10 ^ {12}\ (1\leq i\leq H,1\leq j\leq W) $ - 入力はすべて整数