AT_abc409_c [ABC409C] Equilateral Triangle

There is a circle with circumference $ L $ , and points $ 1,2,\ldots,N $ are placed on this circle. For $ i=1,2,\ldots,N-1 $ , point $ i+1 $ is located at a position that is $ d_i $ clockwise from point $ i $ on the circle. Find the number of integer triples $ (a,b,c)\ (1\leq a\lt b\lt c\leq N) $ that satisfy both of the following conditions: - The three points $ a $ , $ b $ , and $ c $ are all at different positions. - The triangle with vertices at the three points $ a $ , $ b $ , and $ c $ is an equilateral triangle.

The input is given from Standard Input in the following format: > $ N $ $ L $ $ d_1 $ $ d_2 $ $ \ldots $ $ d_{N-1} $

Output the answer.

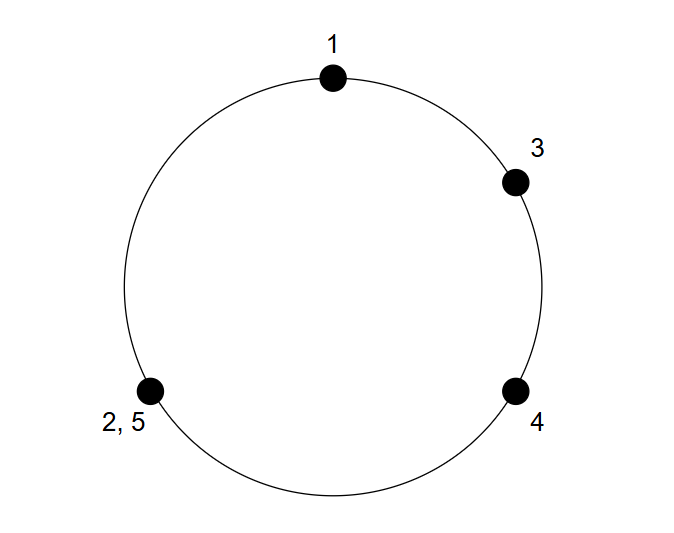
### Sample Explanation 1 The arrangement of the five points is as follows. Two pairs satisfy the conditions: $ (a,b,c)=(1,2,4),(1,4,5) $ .  ### Constraints - $ 3\leq L,N\leq 3\times 10^5 $ - $ 0\leq d_i\lt L $ - All input values are integers.