AT_abc409_c [ABC409C] Equilateral Triangle

円周が $ L $ の円があり、この円周上に点 $ 1,2,\ldots,N $ が配置されています。 $ i=1,2,\ldots,N-1 $ に対し、点 $ i+1 $ は点 $ i $ から時計回りに円周上を $ d_i $ 進んだ位置にあります。 整数の組 $ (a,b,c)\ (1\leq a\lt b\lt c\leq N) $ であって、以下の $ 2 $ つをともに満たすものの個数を求めてください。 - $ 3 $ 点 $ a,b,c $ はすべて異なる位置にある。 - $ 3 $ 点 $ a,b,c $ を頂点とする三角形は正三角形である。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ L $ $ d_1 $ $ d_2 $ $ \ldots $ $ d_{N-1} $

答えを出力せよ。

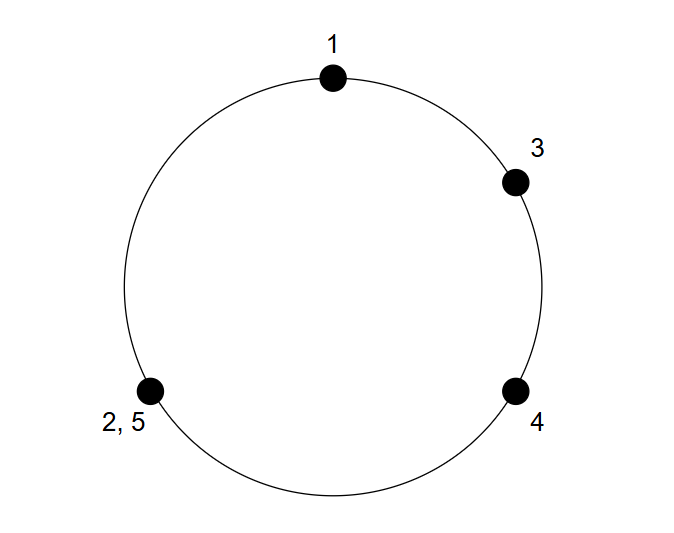
### Sample Explanation 1 $ 5 $ つの点の配置は以下のようになります。条件を満たすのは $ (a,b,c)=(1,2,4),(1,4,5) $ の $ 2 $ つです。  ### Constraints - $ 3\leq L,N\leq 3\times 10^5 $ - $ 0\leq d_i\lt L $ - 入力は全て整数