AT_abc410_g [ABC410G] Longest Chord Chain

There are $ 2N $ pairwise distinct points, numbered from $ 1 $ to $ 2N $ , on a circle. Starting from point $ 1 $ and going clockwise, the points are arranged as point $ 2 $ , point $ 3 $ , ..., point $ 2N $ . You are given $ N $ chords on this circle. The endpoints of the $ i $ -th chord are points $ A_i $ and $ B_i $ , and the $ 2N $ values $ A_1,\ldots,A_N,B_1,\ldots,B_N $ are all distinct. Perform the following operations on this circle once each in order: 1. Among the $ N $ chords on the circle, choose any number of chords such that no two chosen chords intersect, and delete the remaining chords. 2. Add one chord freely to the circle. Find the maximum possible number of intersection points between chords after the operations are completed.

The input is given from Standard Input in the following format: > $ N $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ $ \vdots $ $ A_N $ $ B_N $

Output the answer.

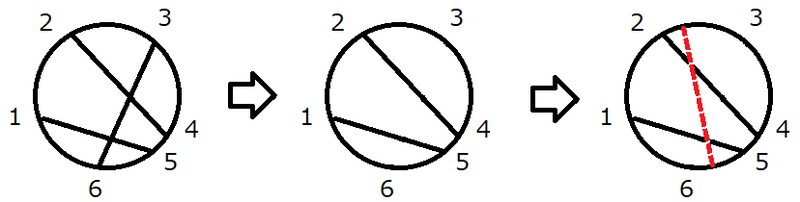
### Sample Explanation 1 Initially, there are $ 3 $ chords on the circle, as shown in the figure. After deleting the chord connecting points $ 3 $ and $ 6 $ and adding a new chord through the operations, the number of intersection points between chords is $ 2 $ .  It is impossible to make the number of intersection points between chords $ 3 $ or more, so the answer is $ 2 $ . The endpoints of the chord added at the end do not need to be any of the points $ 1,\ldots, 2N $ . ### Constraints - $ 1 \leq N \leq 2\times 10^5 $ - $ 1 \leq A_i,B_i \leq 2N $ - The $ 2N $ values $ A_1, \ldots, A_N,B_1,\ldots,B_N $ are pairwise distinct. - All input values are integers.