AT_abc410_g [ABC410G] Longest Chord Chain

円周上に $ 1 $ から $ 2N $ の番号がついた相異なる $ 2N $ 個の点があり、点 $ 1 $ から時計回りに順に点 $ 2 $ 、点 $ 3 $ 、…、点 $ 2N $ と並んでいます。 この円の弦が $ N $ 個与えられます。 $ i $ 番目の弦の端点は点 $ A_i $ と点 $ B_i $ であり、 $ 2N $ 個の値 $ A_1,\ldots,A_N,B_1,\ldots,B_N $ は相異なります。 この円に対し以下の操作を一度ずつ順に行います。 1. 円の $ N $ 本の弦のうち、互いに交わらないように弦を好きな個数選び、残りの弦を削除する。 2. 円に自由に弦を $ 1 $ つ追加する。 適切に操作を行ったとき、操作を終えた後の弦同士の交点の個数として考えられる最大値を求めてください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ $ \vdots $ $ A_N $ $ B_N $

答えを出力せよ。

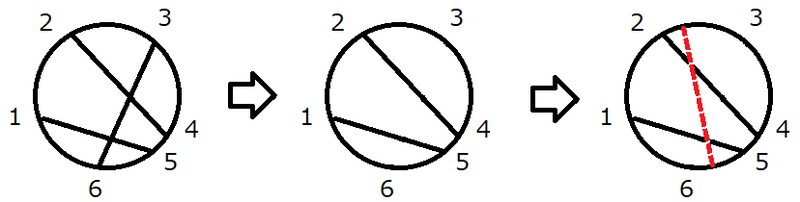
### Sample Explanation 1 最初、円には弦が $ 3 $ 本あり、図のようになっています。 操作により点 $ 3 $ と点 $ 6 $ を結ぶ弦を削除し、新たな弦を追加することで、弦同士の交点の個数は $ 2 $ 個となります。  弦同士の交点の個数を $ 3 $ 個以上にすることはできないため、答えは $ 2 $ となります。 最後に追加する弦の端点は、点 $ 1,\ldots, 2N $ のいずれかである必要はありません。 ### Constraints - $ 1 \leq N \leq 2\times 10^5 $ - $ 1 \leq A_i,B_i \leq 2N $ - $ 2N $ 個の値 $ A_1, \ldots, A_N,B_1,\ldots,B_N $ は相異なる - 入力は全て整数である