AT_abc410_g [ABC410G] Longest Chord Chain

在一个圆上排列着 $2N$ 个点，从点 $1$ 到点 $2N$ 顺时针排列。 给你 $N$ 条弦，第 $i$ 条弦连同点 $A_i,B_i$。保证 $A_1,A_2,\cdots,A_N,B_1,B_2,\cdots,B_N$ 中没有相同的点。 你要执行如下操作： - 选择一个弦的集合保留，删除不在此集合中的所有弦，集合需要满足其中的任意两条弦不存在交点。 - 没有额外限制地在圆上添加一条弦。 求上面两个操作被依次执行后，剩余的所有弦之间最多有多少个交点。

第一行一个整数 $N(1\le N\le 2\times 10^5)$。\ 接下来 $N$ 行，每行两个整数 $A_i,B_i$。

一行一个整数表示答案。

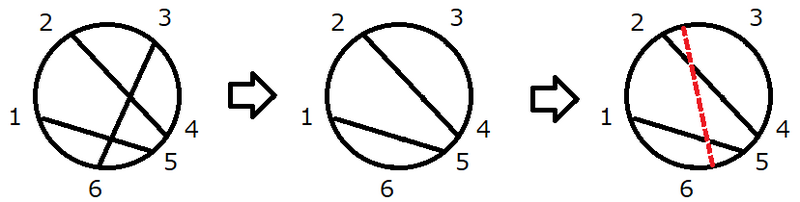
**样例 1 解释** 如图，初始时，圆上有 $3$ 条弦。\ 操作时我们选择删除弦 $(3,6)$ 并加上一条弦，弦之间的交点数为 $2$。  操作后的交点数不可能达到 $3$ 或更多，故答案为 $2$。 并不要求新加的弦的端点在已有的 $2N$ 个点之中。 By @[chenxi2009](/user/1020063)