AT_abc411_f [ABC411F] Contraction

You are given an undirected graph $ G_0 $ with $ N $ vertices and $ M $ edges. The vertices and edges of $ G_0 $ are numbered as vertices $ 1 $ , $ 2 $ , $ \ldots $ , $ N $ and edges $ 1 $ , $ 2 $ , $ \ldots $ , $ M $ , respectively, and edge $ i $ $ (1\leq i\leq M) $ connects vertices $ U_i $ and $ V_i $ . Takahashi has a graph $ G $ and $ N $ pieces numbered as pieces $ 1 $ , $ 2 $ , $ \ldots $ , $ N $ . Initially, $ G=G_0 $ , and piece $ i $ $ (1\leq i\leq N) $ is placed on vertex $ i $ of $ G $ . He will now perform $ Q $ operations in order. The $ i $ -th operation $ (1\leq i\leq Q) $ gives an integer $ X_i $ between $ 1 $ and $ M $ , inclusive, and performs the following operation: > In $ G $ , if pieces $ U_{X_i} $ and $ V_{X_i} $ are placed on different vertices and there exists an edge $ e $ (on $ G $ ) between them, create a graph $ G' $ by contracting that edge. In this case, if self-loops are created, remove them, and if multi-edges exist, replace them with simple edges. > Then, all pieces that were placed on the two vertices connected by edge $ e $ in $ G $ are placed on the newly generated vertex by the contraction of $ e $ in $ G' $ . Pieces that were placed on other vertices in $ G $ are placed on the corresponding vertices in $ G' $ . Finally, set this resulting $ G' $ as the new $ G $ . > If pieces $ U_{X_i} $ and $ V_{X_i} $ are placed on the same vertex, or if the vertices they are placed on are not connected by an edge, do nothing. For each of the operations $ i=1,2,\ldots, Q $ , output the number of edges in $ G $ after the $ i $ -th operation. Edge Contraction Edge contraction of an edge connecting vertices $ u $ and $ v $ is an operation that merges vertices $ u,v $ into one vertex. More precisely, a graph obtained by performing edge contraction on $ G $ refers to the result of performing the following operations on $ G $ : - Add a new vertex $ w $ to $ G $ . - For each vertex $ x $ other than $ u,v $ in $ G $ , if and only if at least one of the edge connecting $ u $ and $ x $ or the edge connecting $ v $ and $ x $ exists, add an edge connecting $ w $ and $ x $ . - Delete vertices $ u,v $ and remove all edges connecting vertices $ u $ and $ v $ , as well as all edges connecting vertex $ u $ or vertex $ v $ with other vertices.

The input is given from Standard Input in the following format: > $ N $ $ M $ $ U_1 $ $ V_1 $ $ U_2 $ $ V_2 $ $ \vdots $ $ U_M $ $ V_M $ $ Q $ $ X_1 $ $ X_2 $ $ \ldots $ $ X_Q $

Output $ Q $ lines. On the $ i $ -th line $ (1\leq i\leq Q) $ , output the number of edges in $ G $ after the $ i $ -th operation.

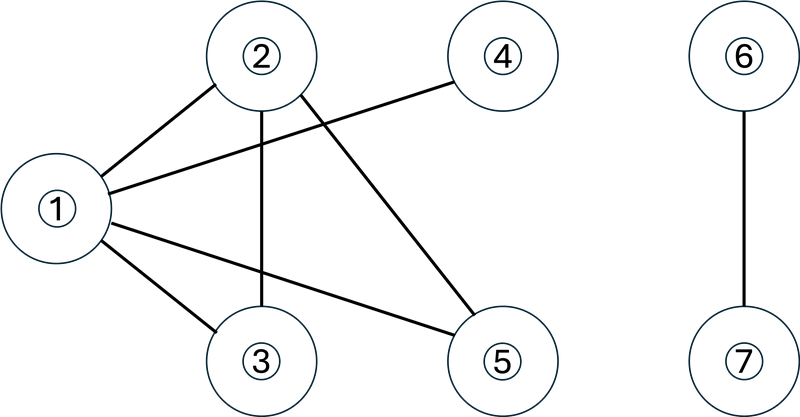
### Sample Explanation 1 Initially, $ G $ is as shown in the figure below. The circled numbers represent pieces with those numbers.  In the $ 1 $ st operation, we contract the edge between the vertices where pieces $ 1 $ and $ 2 $ are placed (left figure below). After the operation, $ G $ becomes as shown in the right figure below, and in particular, the number of edges is $ 4 $ . Note that self-loops have been removed and multi-edges have been replaced with simple edges.  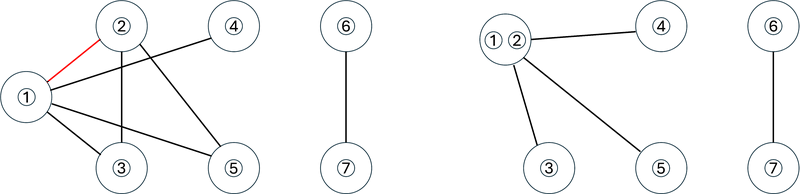In the $ 2 $ nd operation, we contract the edge between the vertices where pieces $ 1 $ and $ 3 $ are placed. After the operation, $ G $ becomes as shown in the left figure below, and the number of edges becomes $ 3 $ . In the $ 3 $ rd operation, since pieces $ 2 $ and $ 3 $ are placed on the same vertex, $ G $ remains unchanged, and the number of edges remains $ 3 $ . In the $ 4 $ th operation as well, since pieces $ 1 $ and $ 2 $ are placed on the same vertex, $ G $ remains unchanged, and the number of edges remains $ 3 $ . 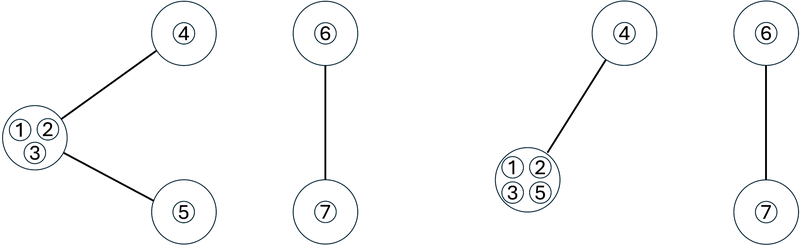In the $ 5 $ th operation, we contract the edge between the vertices where pieces $ 1 $ and $ 5 $ are placed. After the operation, $ G $ becomes as shown in the right figure below, and the number of edges becomes $ 2 $ . Thus, output $ 4,3,3,3,2 $ in this order, separated by newlines.  ### Constraints - $ 2\leq N\leq 3\times 10^5 $ - $ 1\leq M\leq 3\times 10^5 $ - $ 1\leq U_i