AT_abc411_f [ABC411F] Contraction

$ N $ 頂点 $ M $ 辺の無向グラフ $ G_0 $ が与えられます。 $ G_0 $ の頂点および辺は、それぞれ頂点 $ 1 $ , 頂点 $ 2 $ , $ \ldots $ , 頂点 $ N $ および辺 $ 1 $ , 辺 $ 2 $ , $ \ldots $ , 辺 $ M $ と番号づけられており、 辺 $ i $ $ (1\leq i\leq M) $ は頂点 $ U_i $ と頂点 $ V_i $ を結んでいます。 高橋君はグラフ $ G $ と、駒 $ 1 $ , 駒 $ 2 $ , $ \ldots $ , 駒 $ N $ と番号づけられた $ N $ 個の駒を持っています。 最初、 $ G=G_0 $ であり、さらに $ G $ の頂点 $ i $ $ (1\leq i\leq N) $ には駒 $ i $ が置かれています。 高橋君はこれから $ Q $ 回の操作を順に行います。 $ i $ 回目 $ (1\leq i\leq Q) $ の操作では $ 1 $ 以上 $ M $ 以下の整数 $ X_i $ が与えられ、次の操作を行います。 > $ G $ において駒 $ U_{X_i} $ と駒 $ V_{X_i} $ が異なる頂点に置かれており、 それらの間に（ $ G $ 上の）辺 $ e $ が存在するならばその辺を縮約したグラフ $ G' $ を作成する。 この際、自己ループができた場合は取り除き、多重辺が存在した場合は単純辺に置き換える。 > その後、 $ G $ において辺 $ e $ が結んでいた $ 2 $ 頂点に置かれていた駒はすべて、 $ G' $ の $ e $ の縮約によって新たに生成された頂点に置く。 $ G $ 上のその他の頂点に置かれていた駒については、 $ G' $ の対応する頂点に置く。 最後に、このようにしてできた $ G' $ を新たな $ G $ とする。 > 駒 $ U_{X_i} $ と駒 $ V_{X_i} $ が同じ頂点に置かれていた場合、あるいは置かれている頂点の間が辺で結ばれていなかった場合は何も行わない。 $ i=1,2,\ldots, Q $ 回目の操作それぞれについて、 $ i $ 回目の操作の後の $ G $ の辺の数を出力してください。 辺の縮約 とは 頂点 $ u $ と頂点 $ v $ を結ぶ辺の縮約とは、頂点 $ u,v $ を $ 1 $ つの頂点にまとめる操作です。 より正確には、 $ G $ に対して辺の縮約を行なって得られるグラフとは $ G $ に対して次の操作を行って得られるものを指します。 - $ G $ に新たに頂点 $ w $ を追加する。 - $ G $ 上の $ u,v $ 以外の各頂点 $ x $ について、 $ u $ と $ x $ を結ぶ辺、あるいは $ v $ と $ x $ を結ぶ辺の少なくとも一方が存在するとき、かつその時に限り、 $ w $ と $ x $ を結ぶ辺を加える。 - 頂点 $ u,v $ を削除し、頂点 $ u $ と $ v $ を結ぶ辺および頂点 $ u $ または $ v $ と他の頂点を結ぶ辺をすべて削除する。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ M $ $ U_1 $ $ V_1 $ $ U_2 $ $ V_2 $ $ \vdots $ $ U_M $ $ V_M $ $ Q $ $ X_1 $ $ X_2 $ $ \ldots $ $ X_Q $

$ Q $ 行出力せよ。 $ i $ 行目 $ (1\leq i\leq Q) $ には、 $ i $ 回目の操作の後の $ G $ の辺の数を出力せよ。

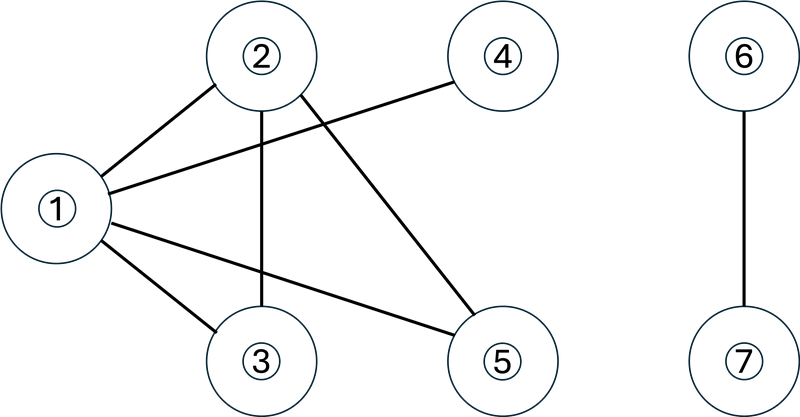
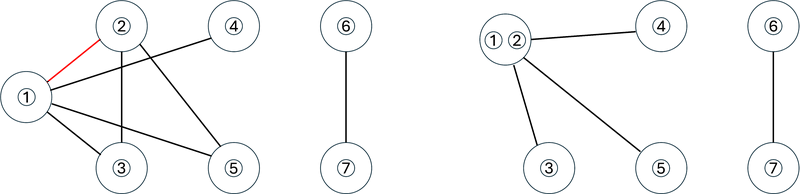
### Sample Explanation 1 最初、 $ G $ は下図のようになっています。丸付き数字はその番号の駒を表します。  $ 1 $ 回目の操作では、駒 $ 1 $ と駒 $ 2 $ が置かれている頂点の間の辺（下図左）の縮約を行います。 操作後、 $ G $ は下図右のようになり、特に辺の数は $ 4 $ です。 自己ループの削除および多重辺の単純辺への置換が行われていることに注意してください。  $ 2 $ 回目の操作では、駒 $ 1 $ と駒 $ 3 $ が置かれている頂点の間の辺の縮約を行います。 操作後、 $ G $ は下図左のようになり、辺の数は $ 3 $ となります。 $ 3 $ 回目の操作では、駒 $ 2 $ と駒 $ 3 $ は同じ頂点に置かれているため、 $ G $ はそのままであり、辺の数も $ 3 $ のままです。 $ 4 $ 回目の操作でも、駒 $ 1 $ と駒 $ 2 $ は同じ頂点に置かれているため、 $ G $ はそのままであり、辺の数も $ 3 $ のままです。 $ 5 $ 回目の操作では、駒 $ 1 $ と駒 $ 5 $ が置かれている頂点の間の辺の縮約を行います。 操作後、 $ G $ は下図右のようになり、辺の数は $ 2 $ となります。 よって、 $ 4,3,3,3,2 $ をこの順に改行区切りで出力します。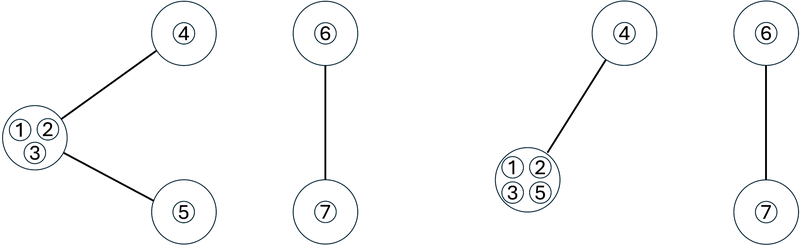  ### Constraints - $ 2\leq N\leq 3\times 10^5 $ - $ 1\leq M\leq 3\times 10^5 $ - $ 1\leq U_i