AT_abc411_f [ABC411F] Contraction

给你一个 $N$ 个点、$M$ 条边的无向图 $G_0$，第 $i$ 条边连接结点 $U_i$ 和结点 $V_i$。 高桥有一个图 $G$ 和 $N$ 个棋子，初始时 $G=G_0$，$i$ 号棋子放在结点 $i$。 他要按顺序执行 $Q$ 次操作。第 $i$ 次操作将给出一个边的编号 $X_i$，并执行以下操作： - 如果棋子 $U_{X_i}$ 和 $V_{X_i}$ 在不同结点上并且这两个结点在 $G$ 中由一条边连接，那么，将 $G$ 中的这条边进行“缩减”得到图 $G'$。如果 $G'$ 中存在重边或自环，将重复的边或自环删除。这条边所连接的两个点上面的所有棋子将被移动到“缩减”操作所创建的新点上。然后 $G\leftarrow G'$。 - 如果两个棋子在相同结点上或者它们所在的两个结点之间没有边，不进行操作。 每次执行操作后，输出图 $G$ 的边数。 - 边的“缩减”：\ 边的缩减是对这条边连接的两个点 $u,v$ 进行合并操作。具体地： - 创建一个新结点 $w$。 - 对于 $G$ 的每个结点 $x\ne u$ 且 $x\ne v$，在 $x$ 和 $w$ 之间连边当且仅当 $x$ 在原图中与 $u$ 有连边，或与 $v$ 有连边。 - 删除 $u,v$ 与和它们两个相连的所有边。

第一行两个整数 $N,M(2\le N\le 3\times 10^5,1\le M\le 3\times 10^5)$。\ 接下来 $M$ 行，每行两个整数 $U_i,V_i(1\le U_i

输出 $Q$ 行，第 $i$ 行输出一个整数表示执行完第 $i$ 个操作后图 $G$ 的边数。

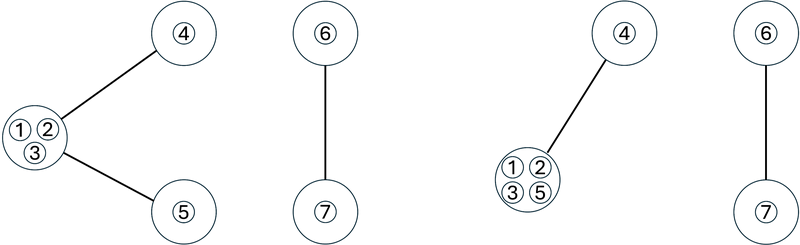
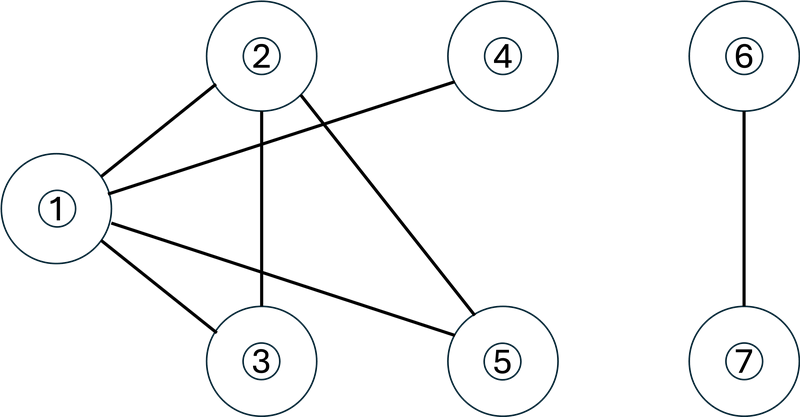
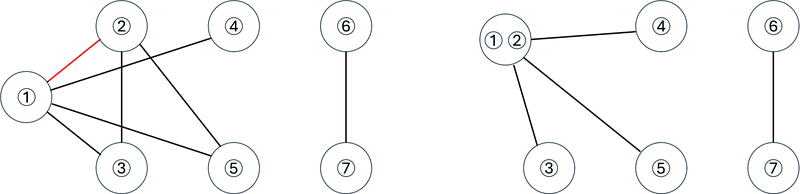
**样例解释** 初始时 $G$ 的状态如图。圈内数字表示点上棋子的编号。  第一次操作我们缩减棋子 $1$ 和棋子 $2$ 所在结点之间的边（左下图）。 操作后，$G$ 如右下图所示，剩余的边数为 $4$。注意自环被删除，重边被一条边代替。  第二次操作缩减棋子 $1$ 和棋子 $3$ 所在结点之间的边。 操作后，$G$ 如左下图所示，剩余的边数为 $3$。 第三次操作时，因为棋子 $2$ 和棋子 $3$ 在同一个结点上，所以图 $G$ 不变。剩余的边数为 $3$。 第四次操作时，因为棋子 $1$ 和棋子 $2$ 在同一个结点上，所以图 $G$ 不变。剩余的边数为 $3$。 第五次操作缩减棋子 $1$ 和棋子 $5$ 所在结点之间的边。 操作后，$G$ 如右下图所示，剩余的边数为 $2$。 因此以此输出 $4,3,3,3,2$。