AT_abc411_g [ABC411G] Count Cycles

给定一个 $N$ 个点、$M$ 条边的无自环的无向图，第 $i$ 条边连通点 $U_i$ 和点 $V_i$，求其中环的个数。 形式化地，找出边集 $\{ e_1,e_2,\cdots,e_k\}\subseteq\{1,2,\cdots,M\}(k\ge 2)$ 的个数，满足 - 存在一个 $(e_1,e_2,\cdots,e_k)$ 的排列 $(e'_1,e'_2,\cdots,e'_k)$ 和一个结点数列 $(v_1,v_2,\cdots,v_k)$，满足： - $v_1,v_2,\cdots,v_k$ 互不相同； - $\forall 1\le i\le k,e'_i$ 连通点 $v_i$ 和点 $v_{(i\bmod N)+1}$。 答案对 $998244353$ 取模。

第一行两个整数 $N,M(2\le N\le 20,2\le M\le 2\times 10^5)$。\ 接下来 $M$ 行，每行两个整数 $U_i,V_i(1\le U_i

一行一个整数输出答案取模后的结果。

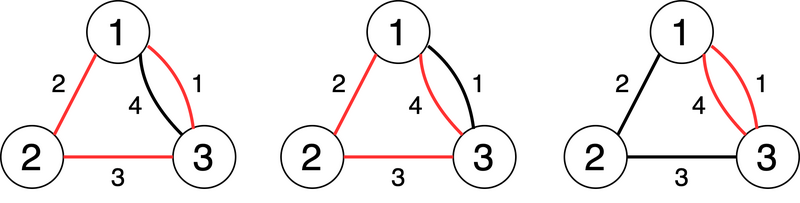
**样例 1 解释** 如图，总共有 $3$ 个环。边旁的数字表示边的编号，红边标记环内的边。  从左到右对应边集 $\{1,2,3\},\{2,3,4\},\{1,4\}$。