AT_abc413_g [ABC413G] Big Banned Grid

There is an $ H \times W $ grid. Let $ (i,j) $ denote the cell at the $ i $ -th row $ (1\le i\le H) $ from the top and $ j $ -th column $ (1\le j\le W) $ from the left. Each cell in the grid either has an obstacle placed on it or has nothing placed on it. There are $ K $ cells with obstacles: cells $ (r_1,c_1),(r_2,c_2),\ldots,(r_K,c_K) $ . Takahashi is initially at cell $ (1,1) $ and wants to reach cell $ (H,W) $ by repeatedly moving to an adjacent cell (up, down, left, right) that has nothing placed on it. More precisely, he can repeat the following operation as many times as he likes: - Choose one of the following four operations and perform the chosen operation: - If $ 1\lt i $ and cell $ (i-1,j) $ has nothing placed on it, move to cell $ (i-1,j) $ . Otherwise, do not move. - If $ 1\lt j $ and cell $ (i,j-1) $ has nothing placed on it, move to cell $ (i,j-1) $ . Otherwise, do not move. - If $ i\lt H $ and cell $ (i+1,j) $ has nothing placed on it, move to cell $ (i+1,j) $ . Otherwise, do not move. - If $ j\lt W $ and cell $ (i,j+1) $ has nothing placed on it, move to cell $ (i,j+1) $ . Otherwise, do not move. Determine whether he can move from cell $ (1,1) $ to cell $ (H,W) $ .

The input is given from standard input in the following format: > $ H $ $ W $ $ K $ $ r_1 $ $ c_1 $ $ r_2 $ $ c_2 $ $ \vdots $ $ r_K $ $ c_K $

If Takahashi can move from cell $ (1,1) $ to cell $ (H,W) $ by repeating the operation described in the problem, print `Yes`; otherwise, print `No`.

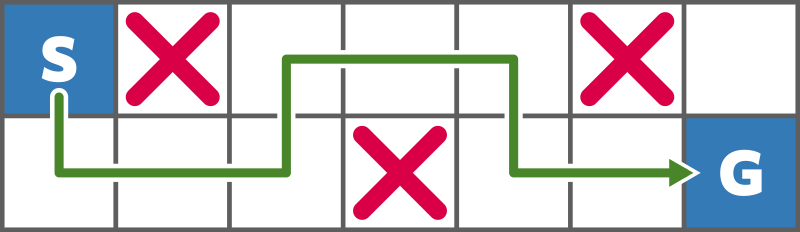
### Sample Explanation 1 The grid looks as follows:  Takahashi cannot move from cell $ (1,1) $ to cell $ (4,5) $ . ### Sample Explanation 2 The grid looks as follows:  He can move from cell $ (1,1) $ to cell $ (2,7) $ by moving as shown in the figure. ### Sample Explanation 3 Note that there may be cases where he does not need to move or where no obstacles are placed. ### Constraints - $ 1\le H\le2\times10^5 $ - $ 1\le W\le2\times10^5 $ - $ 0\le K\le2\times10^5 $ - $ 1\le r_i\le H\ (1\le i\le K) $ - $ 1\le c_i\le W\ (1\le i\le K) $ - $ (r_i,c_i)\ne(1,1)\ (1\le i\le K) $ - $ (r_i,c_i)\ne(H,W)\ (1\le i\le K) $ - $ (r_i,c_i)\ne(r_j,c_j)\ (1\le i\lt j\le K) $ - All input values are integers.