AT_abc413_g [ABC413G] Big Banned Grid
题目描述
有一个 $H\times W$ 的网格,令 $(i,j)$ 表示从上往下第 $i$ 行、从左往右第 $j$ 列的格子。
每个格子上可能放着障碍,也可能是空地。有 $K$ 个格子上放着障碍:$(r_1,c_1),(r_2,c_2),\cdots,(r_K,c_K)$。
高桥在 $(1,1)$ 处,他想要通过不断地移动到相邻的空地来到达 $H,W$。
形式化地,令高桥现在在 $(i,j)$,高桥可以重复以下操作任意次:
- 从以下操作中选择一个执行:
- 如果 $1
输入格式
第一行输入三个整数 $H,W,K(1\le H,W,K\le 2\times 10^5)$。
接下来 $K$ 行,每行输入两个整数 $r_i,c_i(1\le r_i\le H,1\le c_i\le W)$,表示一个障碍,保证没有两个障碍在同一格子上,障碍不会出现在 $(1,1)$ 和 $(H,W)$。
输出格式
如果高桥可以通过不断移动到相邻的格子从 $(1,1)$ 移动到 $(H,W)$,输出 `Yes`;否则输出 `No`。
说明/提示
**样例 1 解释**
网格如下:

高桥不能从 $(1,1)$ 走到 $(H,W)$。
**样例 2 解释**
网格如下:
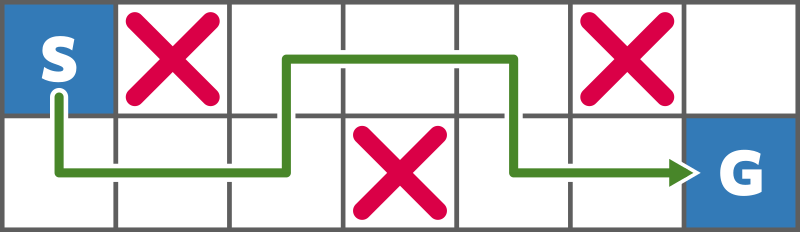
高桥可以通过图示方法从 $(1,1)$ 移动到 $(2,7)$。
**样例 3 解释**
注意有高桥不需要移动或没有任何障碍的情况。