AT_abc417_e [ABC417E] A Path in A Dictionary

给你一个简单相连的无向图 $G$ ，有 $N$ 个顶点和 $M$ 条边。顶点编号从 $1$ 到 $N$，第 $i$ 条边连接点 $U_i$ 和点 $V_i$。 在 $G$ 中，找出从顶点 $X$ 到顶点 $Y$ 的字典序最小的简单路径。 也就是说，在满足以下条件的整数序列 $P=(P_1,P_2,\ldots,P_{\lvert P\rvert})$ 中，找出一条字典序最小的路径： - $1\leq P_i\leq N$ - 若 $i\neq j$ ，则 $P_i\neq P_j$。 - $P_1=X$ 和 $P_{\lvert P\rvert}=Y$。 - 对于 $1\leq i\leq \lvert P\rvert-1$ 来说，存在一条连接顶点 $P_i$ 和 $P_{i+1}$ 的边。 我们可以证明，在此问题的约束条件下，这样一条路径总是存在的。 给你 $T$ 个测试案例，请找出每个案例的答案。 ::::info[整数序列的字典序] 如果下面的任意一个条件成立，则 $S$ 的字典序小于 $T$（下面用 $\lvert S \rvert$ 和 $\lvert T \rvert$ 指代 $S$ 和 $T$ 的长度）： 1. $\lvert S \rvert < \lvert T \rvert$ 且 $(S_1,S_2,\ldots,S_{\lvert S\rvert})=(T_1,T_2,\ldots,T_{\lvert S\rvert})$； 2. 存在一些 $1\leq i\leq \min(\lvert S\rvert,\lvert T\rvert)$，使得 $(S_1,S_2,\ldots,S_{i-1})=(T_1,T_2,\ldots,T_{i-1})$ 且 $S_i

输入从标准输入流按照下列格式给出： > $T$ > $\mathrm{case}_1$ > $\mathrm{case}_2$ > $\vdots$ > $\mathrm{case}_T$ 其中 $\mathrm{case}_i$ 代表第 $i$ 个测试数据，每个测试数据的格式如下： > $N\ M\ X\ Y$ > $U_1\ V_1$ > $U_2\ V_2$ > $\vdots$ > $U_M\ V_M$

输出 $T$ 行。第 $i$ 行为从 $X$ 到 $Y$ 的字典序最小的简单路径，即第 $i$ 个测试数据的答案。 也就是说，如果第 $i$ 个测试数据的答案是 $P=(P_1,P_2,\ldots,P_{\lvert P\rvert})$ 时，在第 $i$ 行一次输出 $P_1$, $P_2$, $\ldots$, $P_{\lvert P\rvert}$，中间用空格隔开。

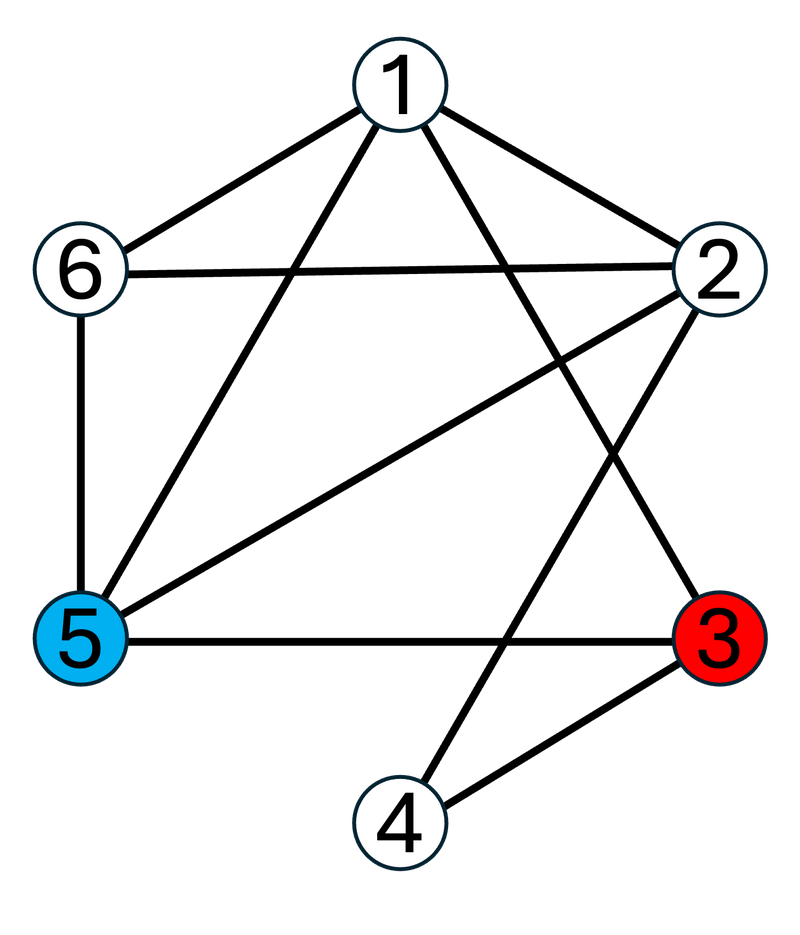
### 数据范围 - $1\leq T\leq 500$ - $2\leq N\leq 1000$ - $N-1\leq M\leq \min\left( \frac{N(N-1)}{2},5\times 10^4\right)$ - $1\leq X,Y \leq N$ - $X\neq Y$ - $1 \leq U_i < V_i \leq N$ - 若 $i\neq j$, 则 $(U_i,V_i)\neq (U_j,V_j)$. - 保证给定图联通 - 每个输入中所有测试数据的 $N$ 之和不超过 $1000$. - 每个输入中所有测试数据的 $M$ 之和不超过 $5\times 10^4$. - 所有输入均为整数. ### 样例解释 对于第一个测试数据，图 $G$ 如下：  在 $G$ 上，从点 $3$ 到点 $5$ 的简单路径按照字典序排列如下： - $(3,1,2,5)$ - $(3,1,2,6,5)$ - $(3,1,5)$ - $(3,1,6,2,5)$ - $(3,1,6,5)$ - $(3,4,2,1,5)$ - $(3,4,2,1,6,5)$ - $(3,4,2,5)$ - $(3,4,2,6,1,5)$ - $(3,4,2,6,5)$ - $(3,5)$ 其中字典序最小的是 $(3,1,2,5)$，因此在第一行输出用空格分隔的 $3,1,2,5$。 对于第二个测试数据，$(3,2)$ 是唯一一条从点 $3$ 到点 $2$ 的简单路径。