AT_abc417_e [ABC417E] A Path in A Dictionary

You are given a simple connected undirected graph $ G $ with $ N $ vertices and $ M $ edges. The vertices of $ G $ are numbered vertex $ 1 $ , vertex $ 2 $ , $ \ldots $ , vertex $ N $ , and the $ i $ -th $ (1\leq i\leq M) $ edge connects vertices $ U_i $ and $ V_i $ . Find the lexicographically smallest simple path from vertex $ X $ to vertex $ Y $ in $ G $ . That is, find the lexicographically smallest among the integer sequences $ P=(P_1,P_2,\ldots,P_{\lvert P\rvert}) $ that satisfy the following conditions: - $ 1\leq P_i\leq N $ - If $ i\neq j $ , then $ P_i\neq P_j $ . - $ P_1=X $ and $ P_{\lvert P\rvert}=Y $ . - For $ 1\leq i\leq \lvert P\rvert-1 $ , there exists an edge connecting vertices $ P_i $ and $ P_{i+1} $ . One can prove that such a path always exists under the constraints of this problem. You are given $ T $ test cases, so find the answer for each. Lexicographic order on integer sequencesAn integer sequence $ S=(S_1,S_2,\ldots,S_{\lvert S\rvert}) $ is lexicographically smaller than an integer sequence $ T=(T_1,T_2,\ldots,T_{\lvert T\rvert}) $ if either of the following 1. or 2. holds. Here, $ \lvert S\rvert $ and $ \lvert T\rvert $ represent the lengths of $ S $ and $ T $ , respectively. 1. $ \lvert S\rvert

The input is given from Standard Input in the following format: > $ T $ $ \mathrm{case}_1 $ $ \mathrm{case}_2 $ $ \vdots $ $ \mathrm{case}_T $ $ \mathrm{case}_i $ represents the $ i $ -th test case. Each test case is given in the following format: > $ N $ $ M $ $ X $ $ Y $ $ U_1 $ $ V_1 $ $ U_2 $ $ V_2 $ $ \vdots $ $ U_M $ $ V_M $

Output $ T $ lines. The $ i $ -th line $ (1\leq i\leq T) $ should contain the vertex numbers on the simple path that is the answer to the $ i $ -th test case, in order, separated by spaces. That is, when the answer to the $ i $ -th test case is $ P=(P_1,P_2,\ldots,P_{\lvert P\rvert}) $ , output $ P_1 $ , $ P_2 $ , $ \ldots $ , $ P_{\lvert P\rvert} $ on the $ i $ -th line in this order, separated by spaces.

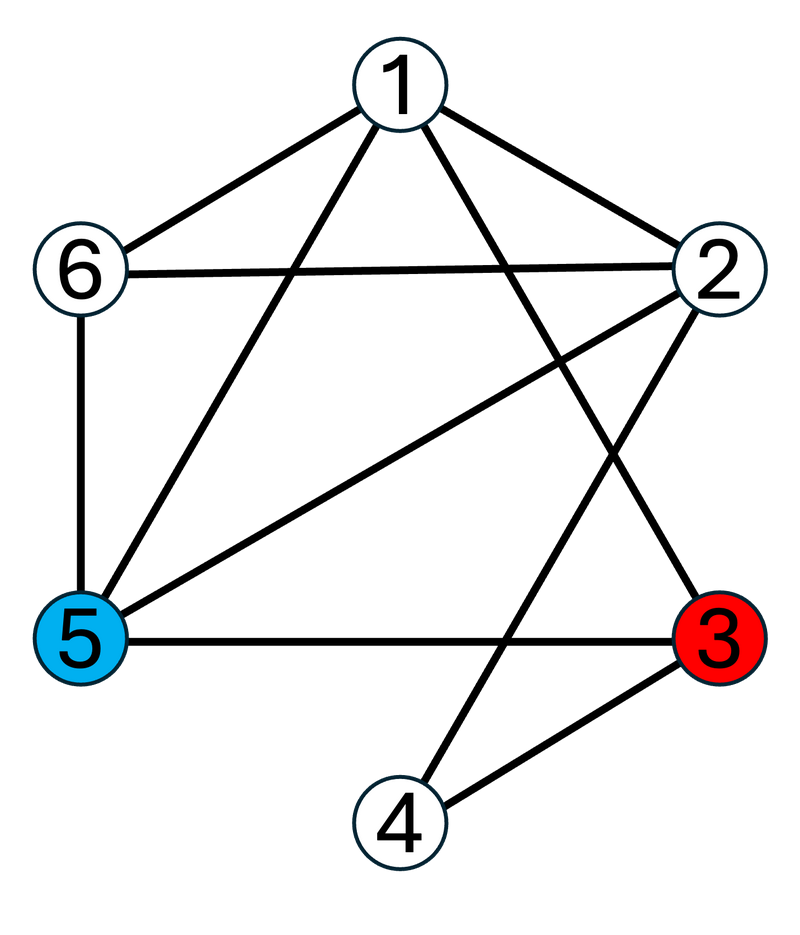
### Sample Explanation 1 For the first test case, graph $ G $ is as follows:  The simple paths from vertex $ 3 $ to vertex $ 5 $ on $ G $ , listed in lexicographic order, are as follows: - $ (3,1,2,5) $ - $ (3,1,2,6,5) $ - $ (3,1,5) $ - $ (3,1,6,2,5) $ - $ (3,1,6,5) $ - $ (3,4,2,1,5) $ - $ (3,4,2,1,6,5) $ - $ (3,4,2,5) $ - $ (3,4,2,6,1,5) $ - $ (3,4,2,6,5) $ - $ (3,5) $ Among these, the lexicographically smallest is $ (3,1,2,5) $ , so output $ 3,1,2,5 $ separated by spaces on the first line. For the second test case, $ (3,2) $ is the only simple path from vertex $ 3 $ to vertex $ 2 $ . ### Constraints - $ 1\leq T\leq 500 $ - $ 2\leq N\leq 1000 $ - $ N-1\leq M\leq \min\left( \frac{N(N-1)}{2},5\times 10^4\right) $ - $ 1\leq X,Y \leq N $ - $ X\neq Y $ - $ 1\leq U_i