AT_abc417_e [ABC417E] A Path in A Dictionary

$ N $ 頂点 $ M $ 辺の単純連結無向グラフ $ G $ が与えられます。 $ G $ の頂点は頂点 $ 1 $ , 頂点 $ 2 $ , $ \ldots $ , 頂点 $ N $ と番号付けられており、 $ i $ $ (1\leq i\leq M) $ 本目の辺は頂点 $ U_i $ と頂点 $ V_i $ を結んでいます。 $ G $ における頂点 $ X $ から頂点 $ Y $ への単純パスのうち辞書順最小のものを求めてください。 すなわち、以下の条件をみたす整数列 $ P=(P_1,P_2,\ldots,P_{\lvert P\rvert}) $ の中で辞書順最小のものを求めてください。 - $ 1\leq P_i\leq N $ - $ i\neq j $ ならば $ P_i\neq P_j $ - $ P_1=X $ かつ $ P_{\lvert P\rvert}=Y $ - $ 1\leq i\leq \lvert P\rvert-1 $ について、頂点 $ P_i $ と頂点 $ P_{i+1} $ を結ぶ辺が存在する。 なお、本問題の制約下で条件をみたすようなものが必ず存在することが証明できます。 $ T $ 個のテストケースが与えられるので、それぞれについて答えを求めてください。 整数列の辞書順 とは整数列 $ S=(S_1,S_2,\ldots,S_{\lvert S\rvert}) $ が整数列 $ T=(T_1,T_2,\ldots,T_{\lvert T\rvert}) $ より辞書順で小さいとは、下記の 1. と 2. のどちらかが成り立つことを言います。 ここで、 $ \lvert S\rvert $ , $ \lvert T\rvert $ はそれぞれ $ S,T $ の長さを表します。 1. $ \lvert S\rvert

入力は以下の形式で標準入力から与えられる。 > $ T $ $ \mathrm{case}_1 $ $ \mathrm{case}_2 $ $ \vdots $ $ \mathrm{case}_T $ $ \mathrm{case}_i $ は $ i $ 番目のテストケースを表す。 各テストケースは以下の形式で与えられる。 > $ N $ $ M $ $ X $ $ Y $ $ U_1 $ $ V_1 $ $ U_2 $ $ V_2 $ $ \vdots $ $ U_M $ $ V_M $

$ T $ 行出力せよ。 $ i $ 行目 $ (1\leq i\leq T) $ には、 $ i $ 個目のテストケースの答えとなる単純パス上の頂点番号を、順に空白区切りで出力せよ。 すなわち $ i $ 個目のテストケースに対する答えが $ P=(P_1,P_2,\ldots,P_{\lvert P\rvert}) $ であるとき、 $ P_1 $ , $ P_2 $ , $ \ldots $ , $ P_{\lvert P\rvert} $ を $ i $ 行目にこの順に空白区切りで出力せよ。

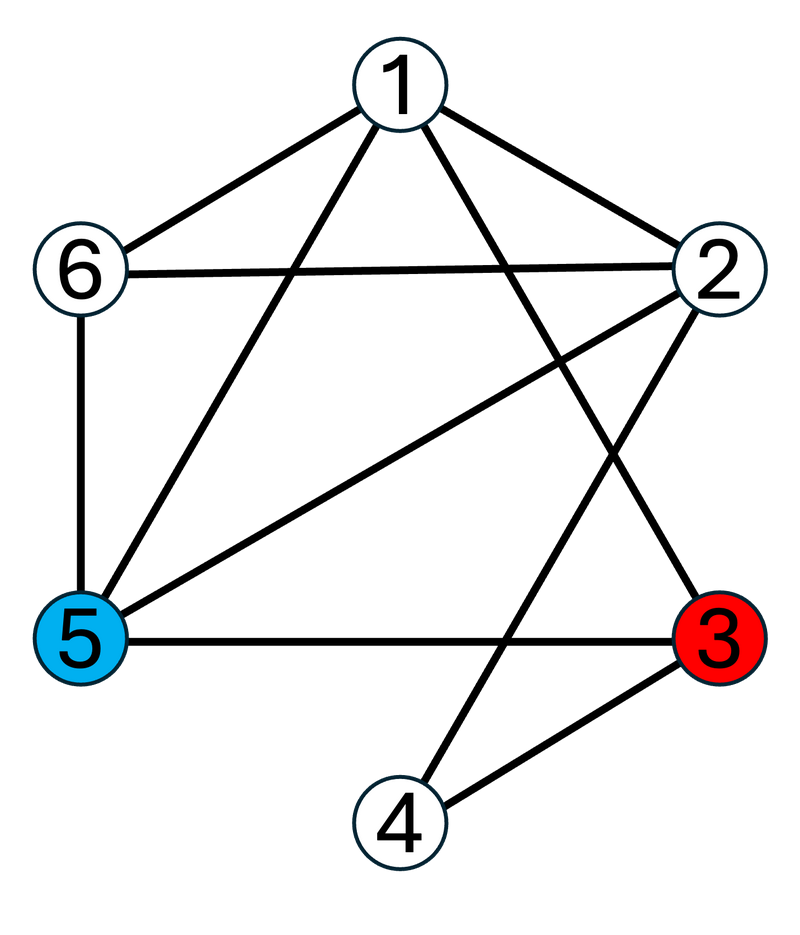
### Sample Explanation 1 $ 1 $ つめのテストケースについて、グラフ $ G $ は次のようになっています。  $ G $ 上の頂点 $ 3 $ から頂点 $ 5 $ への単純パスを辞書順に列挙すると、次のとおりになります。 - $ (3,1,2,5) $ - $ (3,1,2,6,5) $ - $ (3,1,5) $ - $ (3,1,6,2,5) $ - $ (3,1,6,5) $ - $ (3,4,2,1,5) $ - $ (3,4,2,1,6,5) $ - $ (3,4,2,5) $ - $ (3,4,2,6,1,5) $ - $ (3,4,2,6,5) $ - $ (3,5) $ このうち、辞書順最小のものは $ (3,1,2,5) $ であるため、 $ 1 $ 行目には $ 3,1,2,5 $ を空白区切りで出力します。 $ 2 $ つめのテストケースにおいては、 $ (3,2) $ が頂点 $ 3 $ から頂点 $ 2 $ への唯一の単純パスです。 ### Constraints - $ 1\leq T\leq 500 $ - $ 2\leq N\leq 1000 $ - $ N-1\leq M\leq \min\left( \frac{N(N-1)}{2},5\times 10^4\right) $ - $ 1\leq X,Y \leq N $ - $ X\neq Y $ - $ 1\leq U_i