AT_abc418_e [ABC418E] Trapezium

There are $ N $ points on a two-dimensional plane, with the $ i $ -th point at coordinates $ (X_i, Y_i) $ . It is guaranteed that no two points are at the same position, and no three points are collinear. Among the combinations of four points from these points, how many combinations can form a trapezoid as a polygon with those four points as vertices?

The input is given from Standard Input in the following format: > $ N $ $ X_1 $ $ Y_1 $ $ \vdots $ $ X_N $ $ Y_N $

Print the answer on one line.

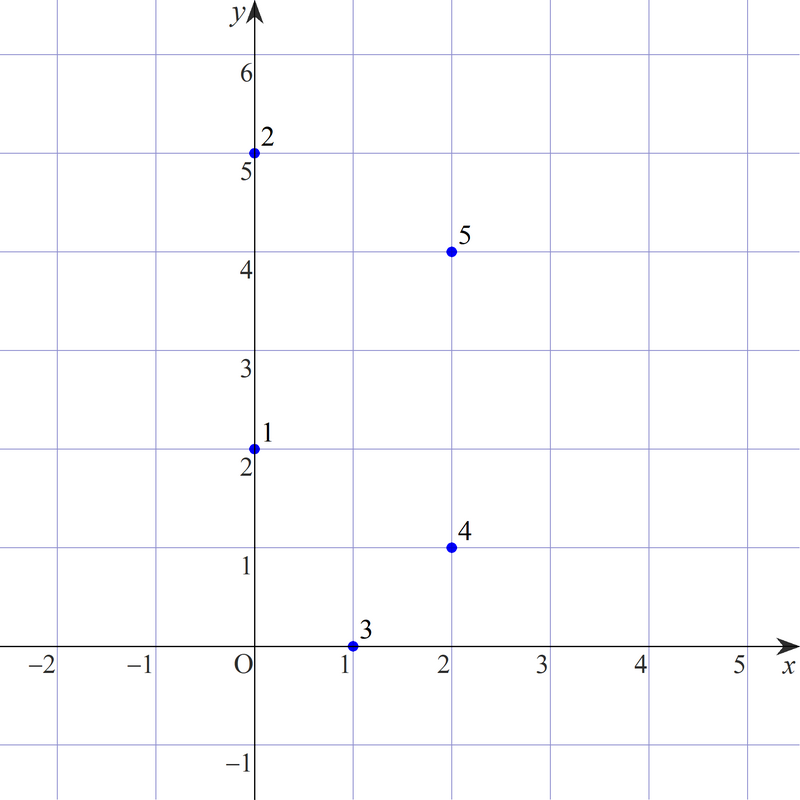
### Sample Explanation 1 The given points are arranged as shown in the figure below.  Among the combinations of four points, the following three combinations can form a trapezoid as a polygon with those points as vertices: - The 1st, 5th, 4th, 3rd points. - The 1st, 3rd, 4th, 2nd points. - The 1st, 2nd, 5th, 4th points. Note that parallelograms and rectangles are also treated as trapezoids. ### Constraints - $ 4 \leq N \leq 2\,000 $ - $ 0 \leq X_i, Y_i \leq 10^7 $ ( $ 1 \leq i \leq N $ ) - No two points are at the same location. - No three points are collinear. - All input values are integers.