AT_abc418_e [ABC418E] Trapezium
Description
二次元平面上に $ N $ 個の点があり、 $ i $ 番目の点は座標 $ (X_i, Y_i) $ にあります。どの $ 2 $ 点も相異なる位置にあり、どの $ 3 $ 点も同一直線上にないことが保証されます。
これらの点から $ 4 $ 点を選ぶ組合せのうち、その $ 4 $ 点を頂点とする多角形として台形がとれるものは何通りありますか?
Input Format
入力は以下の形式で標準入力から与えられる。
> $ N $ $ X_1 $ $ Y_1 $ $ \vdots $ $ X_N $ $ Y_N $
Output Format
答えを $ 1 $ 行に出力せよ。
Explanation/Hint
### Sample Explanation 1
与えられた点は、以下の図のような配置になっています。
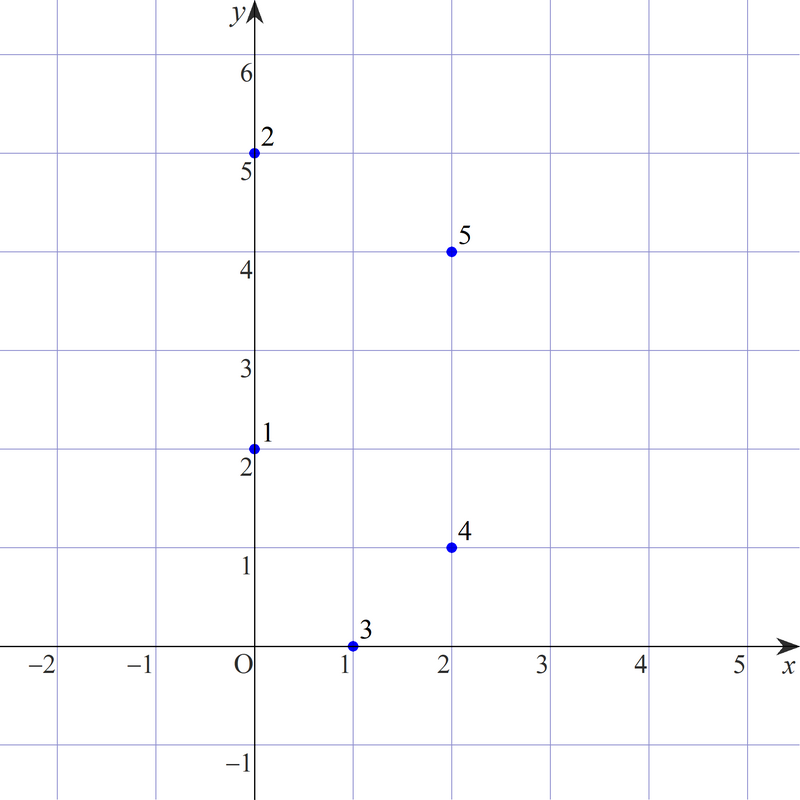
ここから $ 4 $ 点を選ぶ組合せのうち、それらを頂点とする台形がとれるものは以下の $ 3 $ 通りです。
- $ 1,5,4,3 $ 番目の点。
- $ 1,3,4,2 $ 番目の点。
- $ 1,2,5,4 $ 番目の点。
平行四辺形や長方形も台形の一種として扱うことに注意してください。
### Constraints
- $ 4 \leq N \leq 2\,000 $
- $ 0 \leq X_i, Y_i \leq 10^7 $ ( $ 1 \leq i \leq N $ )
- どの $ 2 $ 点も相異なる位置にある。
- どの $ 3 $ 点も同一直線上にない。
- 入力される値は全て整数である。