AT_abc421_d [ABC421D] RLE Moving

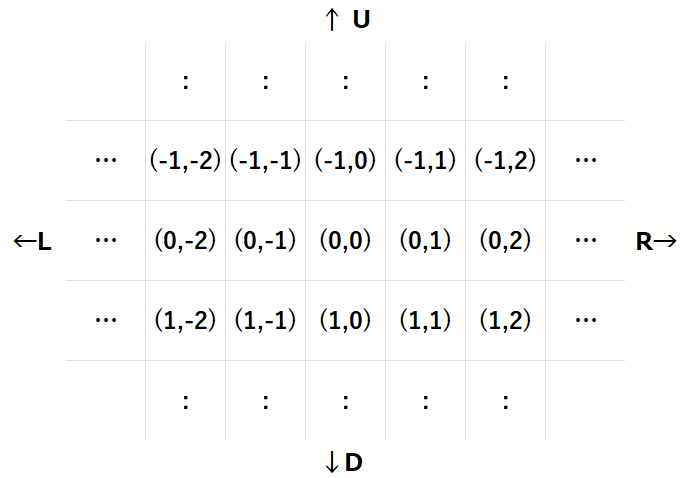
有一个无限大的网格。其中有一个格子被命名为格子 $ (0,0) $。 相对于格子 $ (0,0) $ 向下 $ r $ 格，向右 $ c $ 格的位置称为格子 $ (r,c) $。 这里，“向下 $ r $ 格”表示当 $ r $ 为负时即为“向上 $ |r| $ 格”；“向右 $ c $ 格”表示当 $ c $ 为负时即为“向左 $ |c| $ 格”。 特别地，格子 $ (0,0) $ 周围的格子如下图所示：  一开始，Takahashi 站在格子 $ (R_t,C_t) $，Aoki 站在格子 $ (R_a,C_a) $。他们各自会根据长度为 $ N $ 仅包含 `U`、`D`、`L`、`R` 的字符串 $ S $ 和 $ T $ 移动 $ N $ 步。 对于每一个 $ i $，Takahashi 和 Aoki 的第 $ i $ 步同时进行：若 $ S $ 的第 $ i $ 个字符为 `U`，则 Takahashi 向上一格，若为 `D` 则向下一格，`L` 表示向左一格，`R` 表示向右一格；Aoki 的移动方式与 $ T $ 的第 $ i $ 个字符类似。 请你求出在 $ N $ 次移动过程中，Takahashi 和 Aoki 在某一步移动结束后恰好位于同一个格子的次数。 由于 $ N $ 非常大，$ S $ 和 $ T $ 以如下形式给出：$ ((S'_1, A_1),\ldots,(S'_M,A_M)) $ 和 $ ((T'_1,B_1),\ldots,(T'_L,B_L)) $，其中 $ S $ 为“先连续 $ A_1 $ 次 $ S'_1 $，再连续 $ A_2 $ 次 $ S'_2 $，\dots，最后连续 $ A_M $ 次 $ S'_M $”拼接后的字符串，$ T $ 的描述方式类似。

输入从标准输入读入，格式如下： > $ R_t $ $ C_t $ $ R_a $ $ C_a $ > $ N $ $ M $ $ L $ > $ S'_1 $ $ A_1 $ > $ \vdots $ > $ S'_M $ $ A_M $ > $ T'_1 $ $ B_1 $ > $ \vdots $ > $ T'_L $ $ B_L $

输出答案。

### 样例解释 1 在本样例中，$ S = $ `RRD`，$ T = $ `UUU`，移动过程如下： - 初始时，Takahashi 位于格子 $ (0,0) $，Aoki 位于格子 $ (4,2) $。 - 第 $ 1 $ 步后，Takahashi 位于格子 $ (0,1) $，Aoki 位于格子 $ (3,2) $。 - 第 $ 2 $ 步后，Takahashi 位于格子 $ (0,2) $，Aoki 位于格子 $ (2,2) $。 - 第 $ 3 $ 步后，Takahashi 位于格子 $ (1,2) $，Aoki 位于格子 $ (1,2) $。 因此，Takahashi 和 Aoki 在移动结束后恰好位于同一格子的次数为 $ 1 $。 ### 样例解释 2 从第 $ 2000000000 $ 步到第 $ 3000000000 $ 步，Takahashi 和 Aoki 在每次移动结束后都在同一格子，总共有 $ 1000000001 $ 次。 ### 约束条件 - $ -10^9 \le R_t,C_t,R_a,C_a \le 10^9 $ - $ 1\le N \le 10^{14} $ - $ 1\le M,L \le 10^5 $ - 每个 $ S'_i $ 和 $ T'_i $ 均为 `U`、`D`、`L`、`R` 之一。 - $ 1 \le A_i,B_i \le 10^9 $ - $ A_1+\dots+A_M=B_1+\dots+B_L=N $ - 所有给定数值均为整数。 由 ChatGPT 5 翻译