AT_abc422_f [ABC422F] Eat and Ride

有一个包含 $N$ 个顶点和 $M$ 条边的无向连通图，顶点编号为 $1,2,\ldots,N$，第 $i$ 条边（$1\le i\le M$）连接顶点 $u_i$ 和 $v_i$。 对于 $i=1,2,\ldots,N$，请解决以下问题： 初始时，高桥的体重为 $0$。 他乘车前往访问顶点 $1$，并向着顶点 $i$ 前进。当他访问顶点 $v$（$1\le v\le N$）时，他的体重会增加 $W_v$。 他所乘坐的汽车可以沿着边行驶。当他通过一条边时，假设此时体重为 $X$，则会消耗 $X$ 的燃料。 求他到达顶点 $i$ 时所需消耗的燃料的最小值。

输入通过标准输入给出，格式如下： >$N$ $M$ > >$W_1$ $W_2$ $\ldots$ $W_N$ > >$u_1$ $v_1$ > >$u_2$ $v_2$ > >$\vdots$ > >$u_M$ $v_M$

输出共 $N$ 行。第 $i$ 行（$1\le i\le N$）输出高桥到达顶点 $i$ 所需消耗的燃料值。

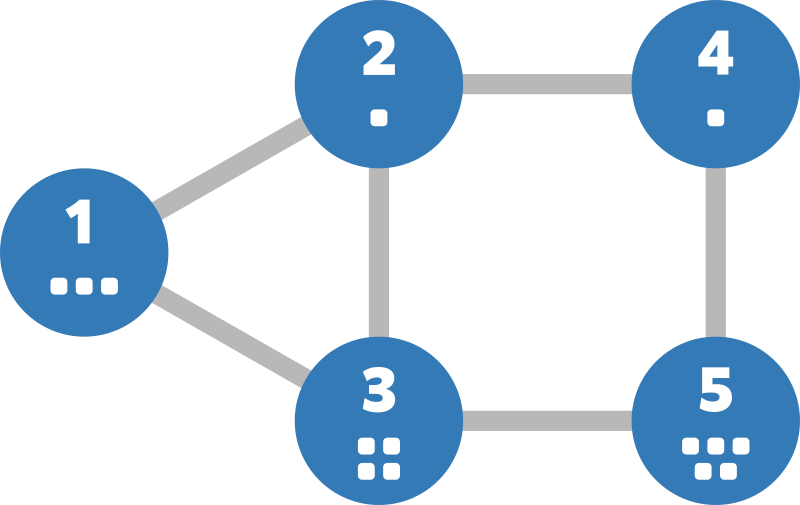
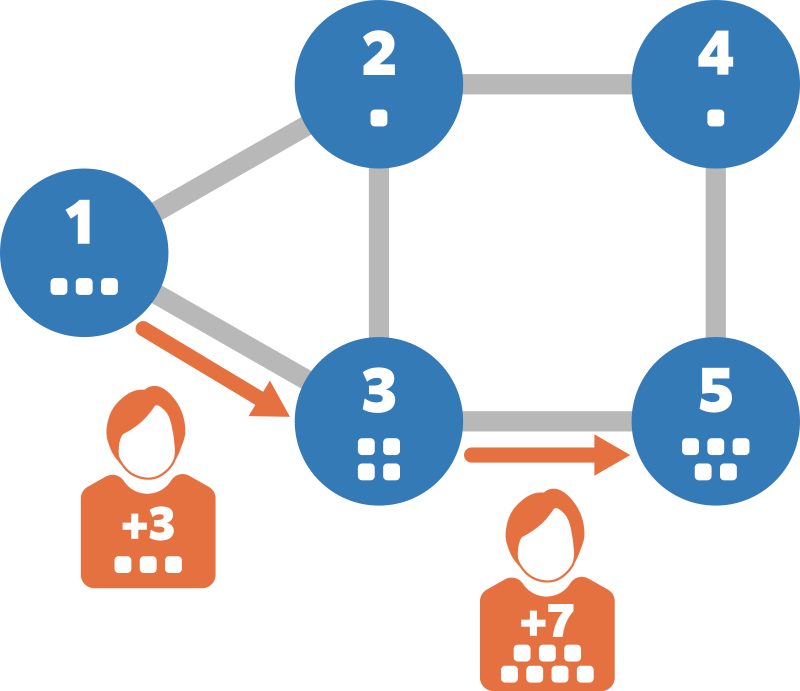
### 样例解释 1 给定的图如下所示：  例如，高桥可以按以下方式访问顶点 $5$： - 访问顶点 $1$，体重增加 $3$，变为 $3$。 - 消耗 $3$ 单位燃料移动到顶点 $3$，体重增加 $4$，变为 $7$。 - 消耗 $7$ 单位燃料移动到顶点 $5$，体重增加 $5$，变为 $12$。  这样他可以消耗 $10$ 单位燃料到达顶点 $5$。不可能将燃料消耗降到 $9$ 或更少，所以请在第 $5$ 行输出 $10$。 ### 样例解释 2 注意答案可能会超过 $2^{32}$。 ### 数据范围 - $1\le N\le5000$ - $1\le M\le5000$ - $1\le W_i\le10^9\ (1\le i\le N)$ - $1\le u_i\le v_i\le N\ (1\le i\le M)$ - 给定的图是连通的。 - 所有输入数据均为整数。 由 ChatGPT 5 翻译