AT_abc422_f [ABC422F] Eat and Ride

There is a connected undirected graph with $ N $ vertices and $ M $ edges. The vertices are numbered vertex $ 1, $ vertex $ 2,\ldots, $ vertex $ N $ , and the $ i $ -th edge $ (1\le i\le M) $ connects vertices $ u _ i $ and $ v _ i $ . For $ i=1,2,\ldots,N $ , solve the following problem: Initially, Takahashi's weight is $ 0 $ . He travels by car to visit vertex $ 1 $ and moves toward vertex $ i $ . When he visits vertex $ v\ (1\le v\le N) $ , his weight increases by $ W _ v $ . The car he is riding can move along the edges. When he passes through an edge, letting $ X $ be his weight at that time, the car consumes $ X $ fuel. Find the minimum amount of fuel consumed for him to reach vertex $ i $ .

The input is given from Standard Input in the following format: > $ N $ $ M $ $ W _ 1 $ $ W _ 2 $ $ \ldots $ $ W _ N $ $ u _ 1 $ $ v _ 1 $ $ u _ 2 $ $ v _ 2 $ $ \vdots $ $ u _ M $ $ v _ M $

Output over $ N $ lines. On the $ i $ -th line $ (1\le i\le N) $ , output the amount of fuel needed for Takahashi to reach vertex $ i $ .

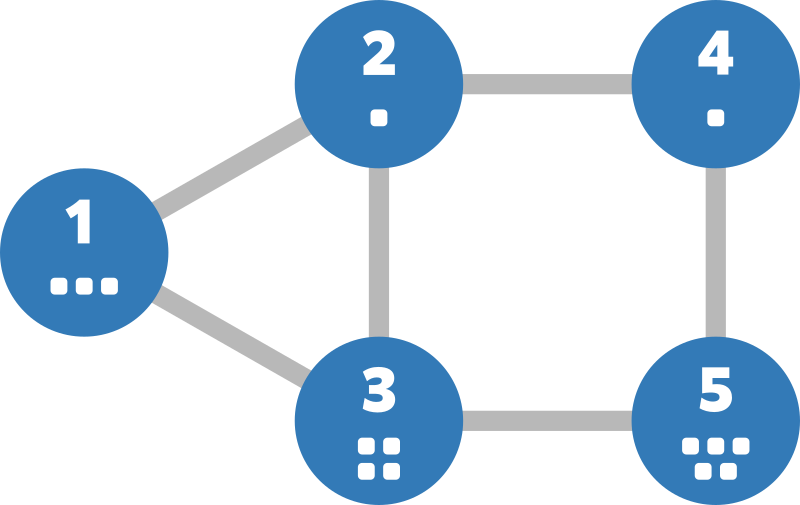
### Sample Explanation 1 The given graph is as follows:  For example, Takahashi can reach vertex $ 5 $ by visiting vertex $ 1 $ and then acting as follows: - He visits vertex $ 1 $ . His weight increases by $ 3 $ , becoming $ 3 $ . - He consumes $ 3 $ fuel to move to vertex $ 3 $ . His weight increases by $ 4 $ , becoming $ 7 $ . - He consumes $ 7 $ fuel to move to vertex $ 5 $ . His weight increases by $ 5 $ , becoming $ 12 $ .  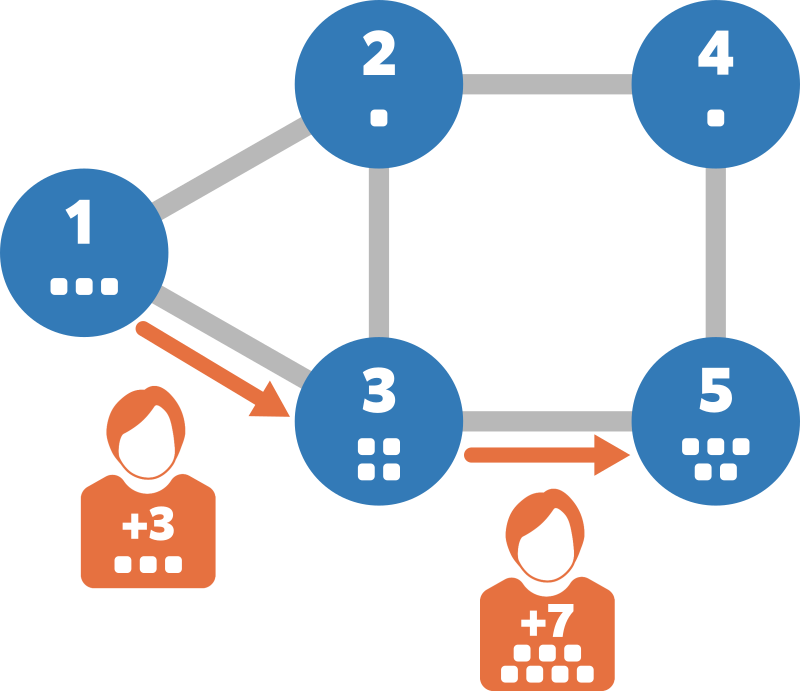By acting this way, he can reach vertex $ 5 $ by consuming $ 10 $ fuel. It is impossible to reduce the fuel consumption to $ 9 $ or less, so output $ 10 $ on the $ 5 $ th line. ### Sample Explanation 2 Note that the answer may exceed $ 2 ^ {32} $ . ### Constraints - $ 1\le N\le5000 $ - $ 1\le M\le5000 $ - $ 1\le W _ i\le10 ^ 9\ (1\le i\le N) $ - $ 1\le u _ i\le v _ i\le N\ (1\le i\le M) $ - The given graph is connected. - All input values are integers.