AT_abc422_f [ABC422F] Eat and Ride

$ N $ 頂点 $ M $ 辺の連結無向グラフがあります。 頂点には頂点 $ 1, $ 頂点 $ 2,\ldots, $ 頂点 $ N $ と番号付けられており、 $ i $ 番目 $ (1\le i\le M) $ の辺は頂点 $ u _ i $ と頂点 $ v _ i $ を結んでいます。 $ i=1,2,\ldots,N $ について次の問題を解いてください。 はじめ、高橋くんの体重は $ 0 $ です。 高橋くんは、車に乗って頂点 $ 1 $ に訪れ、頂点 $ i $ に向かって移動を行います。 高橋くんが頂点 $ v\ (1\le v\le N) $ に訪れるとき、高橋くんの体重は $ W _ v $ だけ増加します。 高橋くんが乗っている車は辺に沿って移動することができます。 高橋くんが辺を通過するとき、そのときの高橋くんの体重を $ X $ として、車は燃料を $ X $ 消費します。 高橋くんが頂点 $ i $ にたどり着くために消費する燃料の量の最小値を求めてください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ M $ $ W _ 1 $ $ W _ 2 $ $ \ldots $ $ W _ N $ $ u _ 1 $ $ v _ 1 $ $ u _ 2 $ $ v _ 2 $ $ \vdots $ $ u _ M $ $ v _ M $

$ N $ 行にわたって出力せよ。 $ i $ 行目 $ (1\le i\le N) $ には、高橋くんが頂点 $ i $ にたどり着くのに必要な燃料の量を出力せよ。

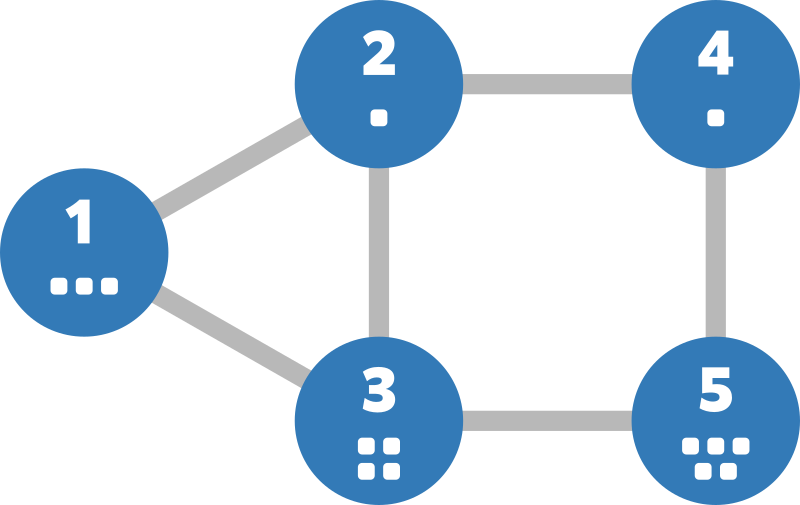
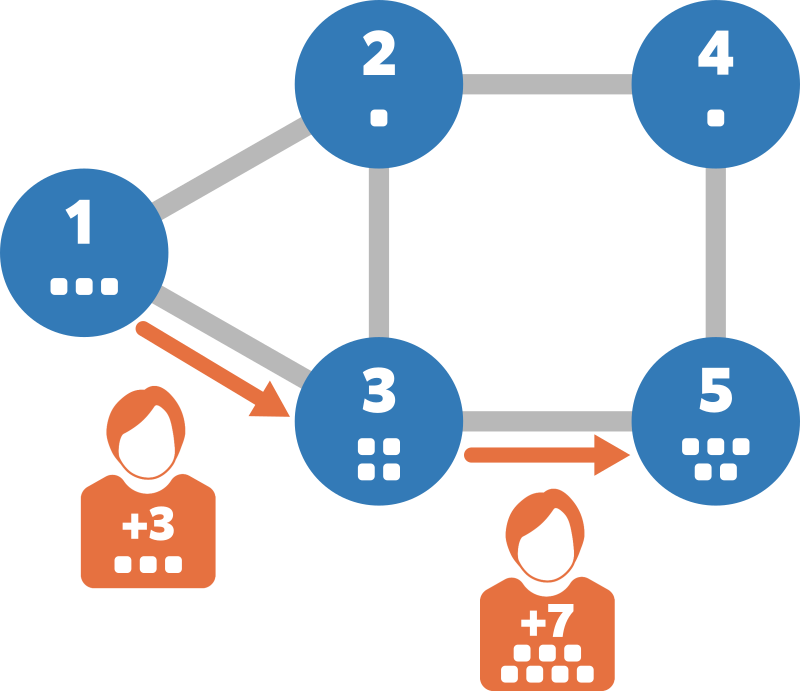
### Sample Explanation 1 与えられたグラフは以下のようになります。  例えば、高橋くんは頂点 $ 1 $ に訪れてから次のように行動することで頂点 $ 5 $ にたどり着くことができます。 - 高橋くんが頂点 $ 1 $ に訪れる。高橋くんの体重が $ 3 $ 増加し、 $ 3 $ になる。 - 高橋くんが燃料を $ 3 $ 消費して頂点 $ 3 $ に移動する。高橋くんの体重が $ 4 $ 増加し、 $ 7 $ になる。 - 高橋くんが燃料を $ 7 $ 消費して頂点 $ 5 $ に移動する。高橋くんの体重が $ 5 $ 増加し、 $ 12 $ になる。  このように行動することで燃料を $ 10 $ だけ消費して頂点 $ 5 $ にたどり着くことができます。 消費する燃料を $ 9 $ 以下にすることはできないため、 $ 5 $ 行目には $ 10 $ を出力してください。 ### Sample Explanation 2 答えが $ 2 ^ {32} $ を越える場合があることに注意してください。 ### Constraints - $ 1\le N\le5000 $ - $ 1\le M\le5000 $ - $ 1\le W _ i\le10 ^ 9\ (1\le i\le N) $ - $ 1\le u _ i\le v _ i\le N\ (1\le i\le M) $ - 与えられるグラフは連結 - 入力はすべて整数