AT_abc424_f [ABC424F] Adding Chords

There are $ N $ points equally spaced on a circle, numbered $ 1,2,\dots,N $ clockwise. You are given $ Q $ queries of the following form; process them in order. - Draw the line segment connecting points $ A_i $ and $ B_i $ . However, if this segment intersects a segment that has already been drawn, do not draw it. Here, it is guaranteed that the $ 2Q $ integers $ A_1,\ldots,A_Q,B_1,\ldots,B_Q $ are all distinct. For each query, answer whether the segment was drawn.

The input is given from Standard Input in the following format: > $ N $ $ Q $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ $ \vdots $ $ A_Q $ $ B_Q $

Output $ Q $ lines. On the $ i $ -th line, output `Yes` if, in the $ i $ -th query, the segment was drawn, and `No` if it was not drawn.

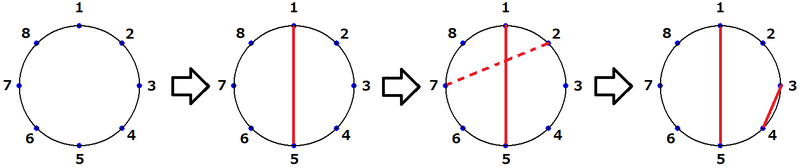
### Sample Explanation 1 By the queries, the segments are drawn as in the figure. - In the $ 1 $ -st query, the segment connecting points $ 1 $ and $ 5 $ is drawn. - In the $ 2 $ -nd query, the segment connecting points $ 2 $ and $ 7 $ is not drawn because it intersects the segment drawn in the $ 1 $ -st query. - In the $ 3 $ -rd query, the segment connecting points $ 3 $ and $ 4 $ is drawn.  ### Constraints - $ 2 \leq N \leq 10^6 $ - $ 1 \leq Q \leq 3\times 10^5 $ - $ 1 \leq A_i < B_i \leq N $ - The $ 2Q $ integers $ A_1,\ldots,A_Q,B_1,\ldots,B_Q $ are pairwise distinct. - All input values are integers.