AT_abc425_d [ABC425D] Ulam-Warburton Automaton

有一个有 $H$ 行 $W$ 列的网格。我们称自上而下第 $i$ 行 $(1 \leq i \leq H)$、自左而右第 $j$ 列 $(1 \leq j \leq W)$ 交汇处的格子为 $(i,j)$。 初始时，如果 $S_{i,j}$ 为 `#`，则 $(i,j)$ 被染成黑色；如果为 `.`，则 $(i,j)$ 被染成白色。 执行下面的操作 $10^{100}$ 次： - 令 $T$ 为所有仅有一个相邻黑色格子的白色格子的集合。将这些格子全部染成黑色。这里，两个格子 $(i_1, j_1)$ 和 $(i_2, j_2)$ 相邻当且仅当 $|i_1 - i_2| + |j_1 - j_2| = 1$。 请你求出所有操作完成后被染成黑色的格子的数量。

输入从标准输入读取，格式如下： > $H\ W$ > $S_{1,1}S_{1,2}\ldots S_{1,W}$ > $S_{2,1}S_{2,2}\ldots S_{2,W}$ > $\vdots$ > $S_{H,1}S_{H,2}\ldots S_{H,W}$

输出答案。

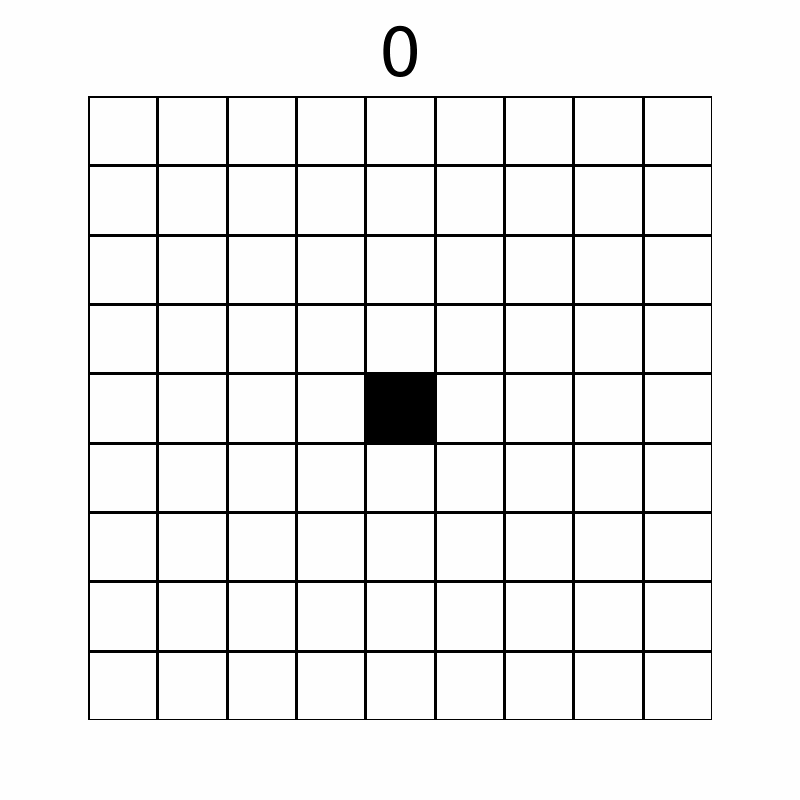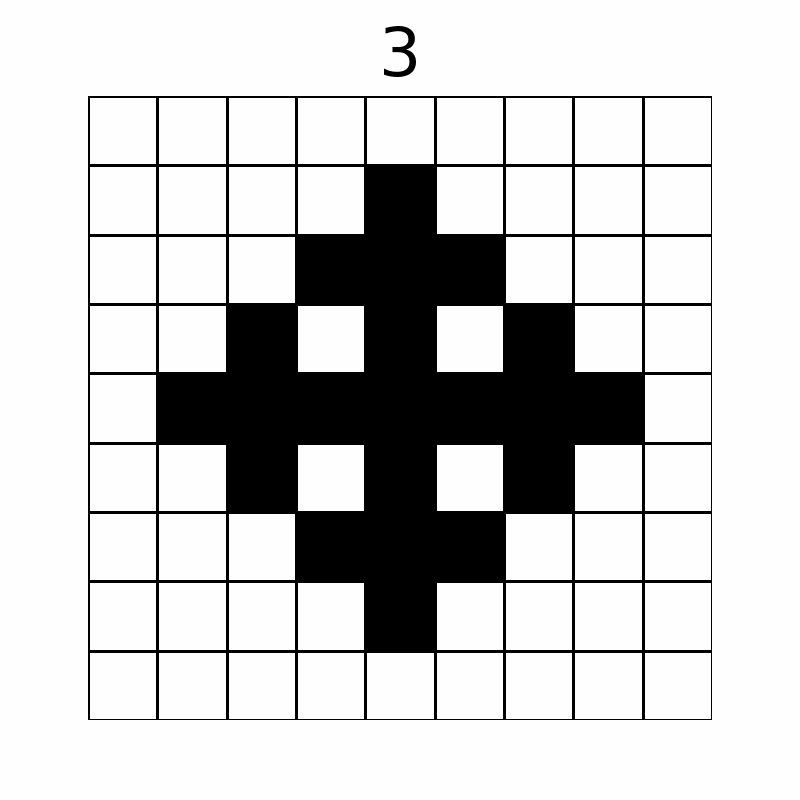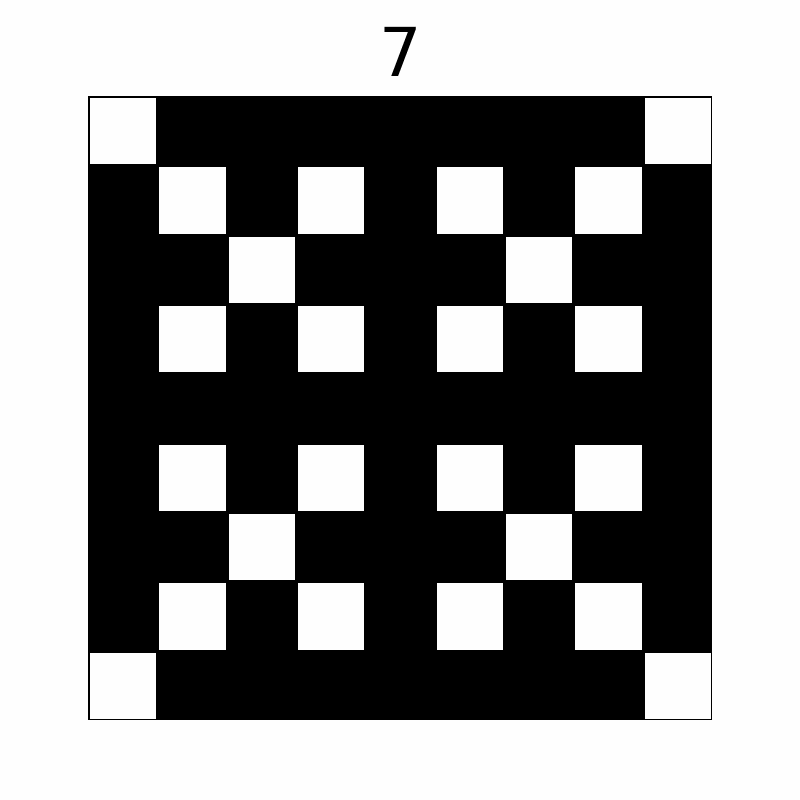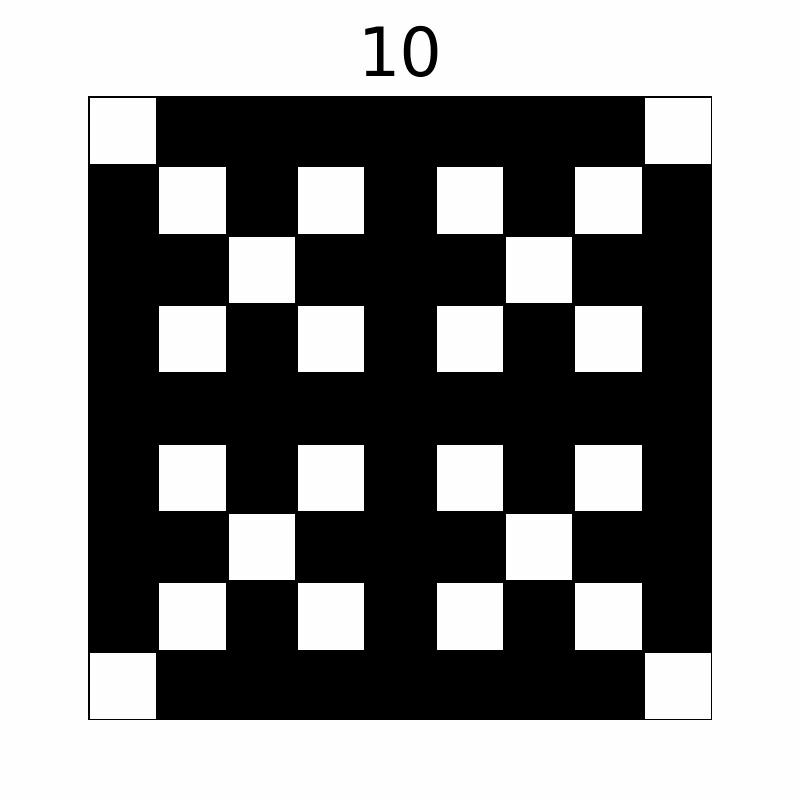
### 样例解释 1 经过如下所示几轮操作，网格状态会发生变化。（上方数字为操作次数，前十轮操作显示如下）  最终，共有 $57$ 个格子变成了黑色。 ### 数据范围 - $2 \leq H, W$ - $HW \leq 3 \times 10^5$ - $H$ 和 $W$ 为整数。 - $S_{i,j}$ 只能为 `#` 或 `.`。 由 ChatGPT 5 翻译