AT_abc425_d [ABC425D] Ulam-Warburton Automaton

There is a grid with $ H $ rows and $ W $ columns. We call the cell at the $ i $ -th row from the top $ (1\leq i\leq H) $ and $ j $ -th column from the left $ (1\leq j\leq W) $ as cell $ (i,j) $ . Initially, cell $ (i,j) $ is colored black if $ S_{i,j} $ is `#` and white if it is `.`. Perform the following operation $ 10^{100} $ times: - Let $ T $ be the set of cells that are colored white and have exactly one adjacent cell colored black. Color each cell in $ T $ black. Here, two cells $ (i_1,j_1) $ and $ (i_2,j_2) $ are adjacent if and only if $ |i_1-i_2|+|j_1-j_2|=1 $ . Find the number of cells that are colored black after all operations are completed.

The input is given from Standard Input in the following format: > $ H $ $ W $ $ S_{1,1}S_{1,2}\ldots S_{1,W} $ $ S_{2,1}S_{2,2}\ldots S_{2,W} $ $ \vdots $ $ S_{H,1}S_{H,2}\ldots S_{H,W} $

Output the answer.

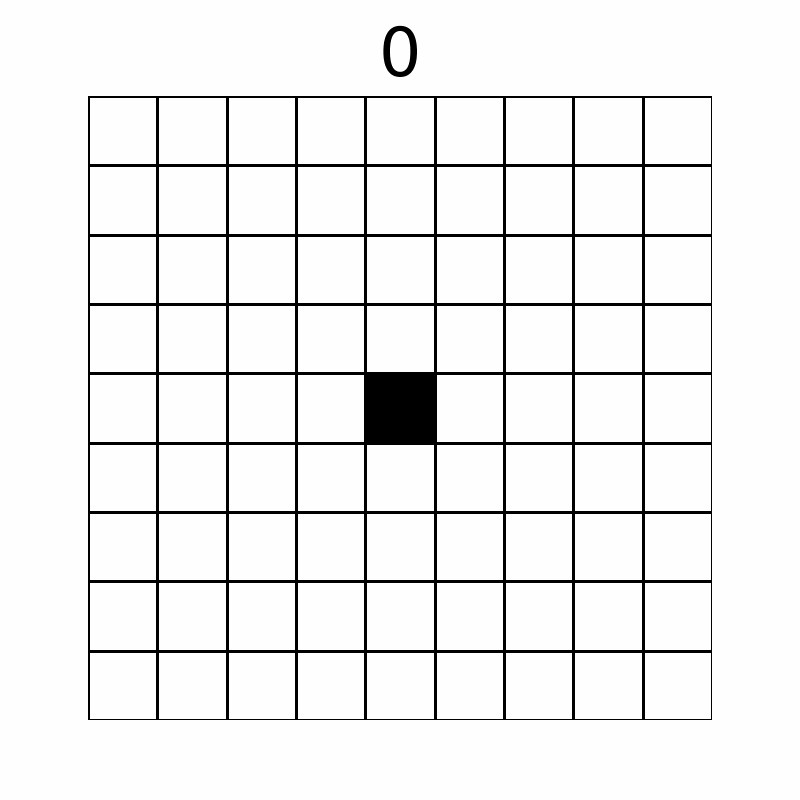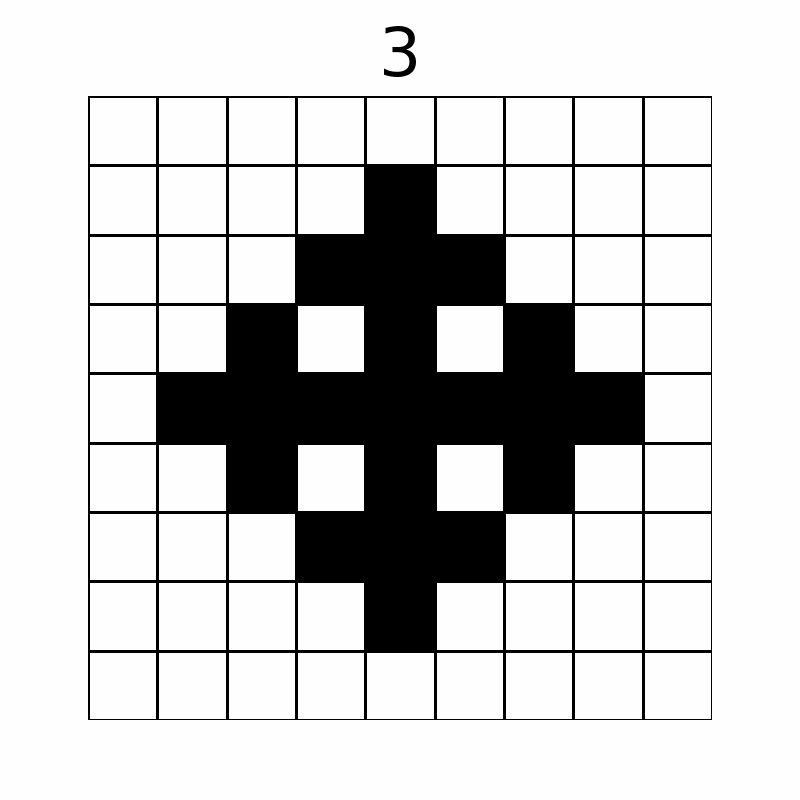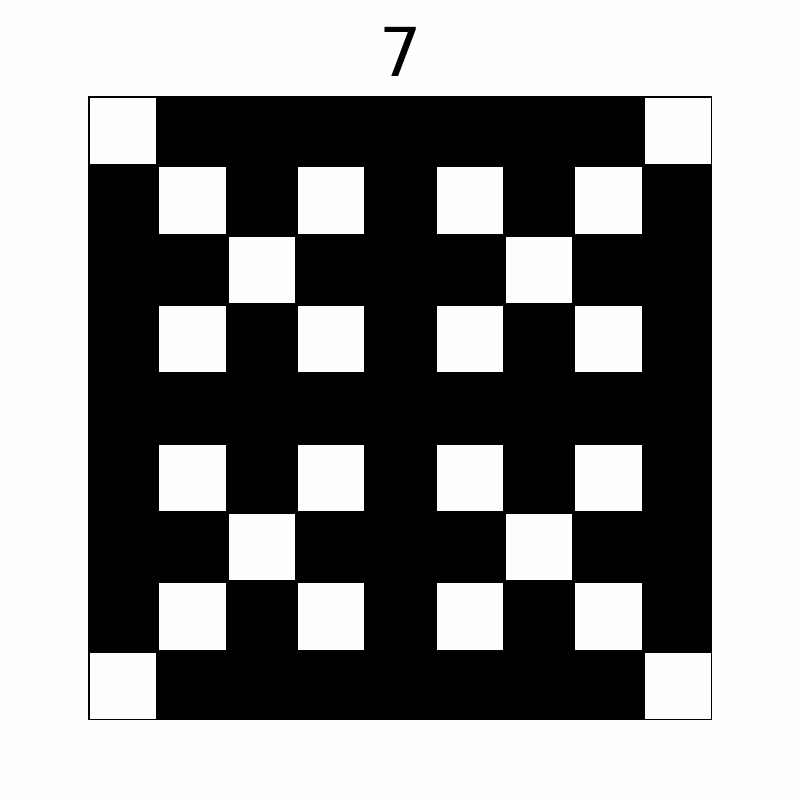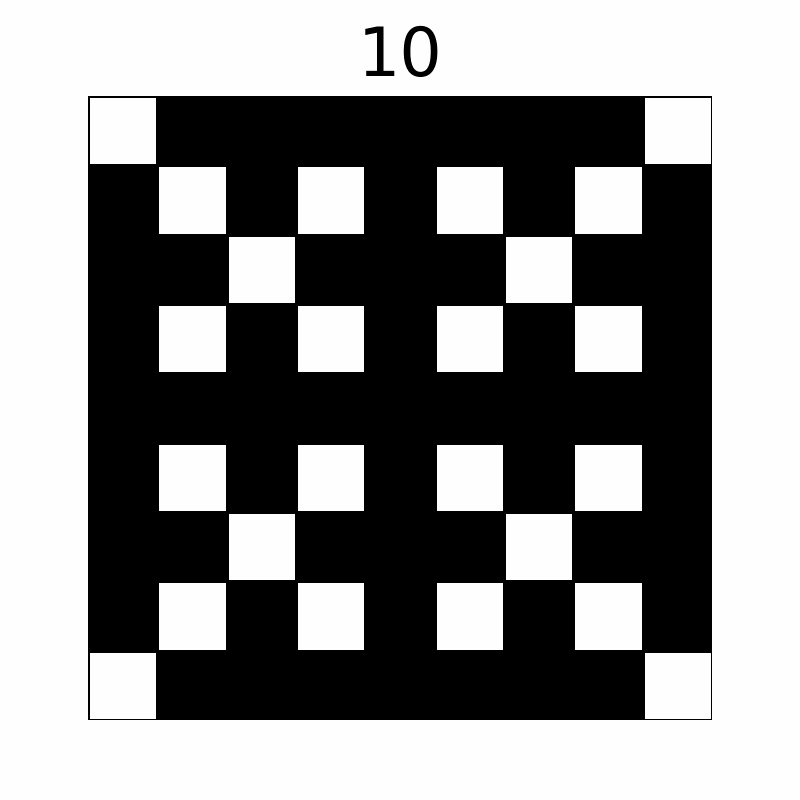
### Sample Explanation 1 The grid changes as follows through the operations. (The number above represents the operation count. The first ten operations are displayed.)  Eventually, $ 57 $ cells are colored black. ### Constraints - $ 2\leq H,W $ - $ HW\leq 3\times 10^5 $ - $ H $ and $ W $ are integers. - $ S_{i,j} $ is `#` or `.`.