AT_abc425_d [ABC425D] Ulam-Warburton Automaton

$ H $ 行 $ W $ 列のマス目があります。上から $ i $ 行目 $ (1\leq i\leq H) $ 、左から $ j $ 列目 $ (1\leq j\leq W) $ のマスをマス $ (i,j) $ と呼ぶことにします。 はじめ、マス $ (i,j) $ は $ S_{i,j} $ が `#` のとき黒、`.` のとき白で塗られています。 以下の操作を $ 10^{100} $ 回行います。 - 白で塗られているマスであって、そのマスに辺で隣接するマスのうちちょうど $ 1 $ つが黒で塗られているようなマスの集合を $ T $ とする。 $ T $ の各マスに対して、そのマスを黒で塗る。ただし、 $ 2 $ つのマス $ (i_1,j_1),(i_2,j_2) $ が辺で隣接するとは、 $ |i_1-i_2|+|j_1-j_2|=1 $ であることをいう。 すべての操作が終わったあとに黒く塗られているマスの個数を求めてください。

入力は以下の形式で標準入力から与えられる。 > $ H $ $ W $ $ S_{1,1}S_{1,2}\ldots S_{1,W} $ $ S_{2,1}S_{2,2}\ldots S_{2,W} $ $ \vdots $ $ S_{H,1}S_{H,2}\ldots S_{H,W} $

答えを出力せよ。

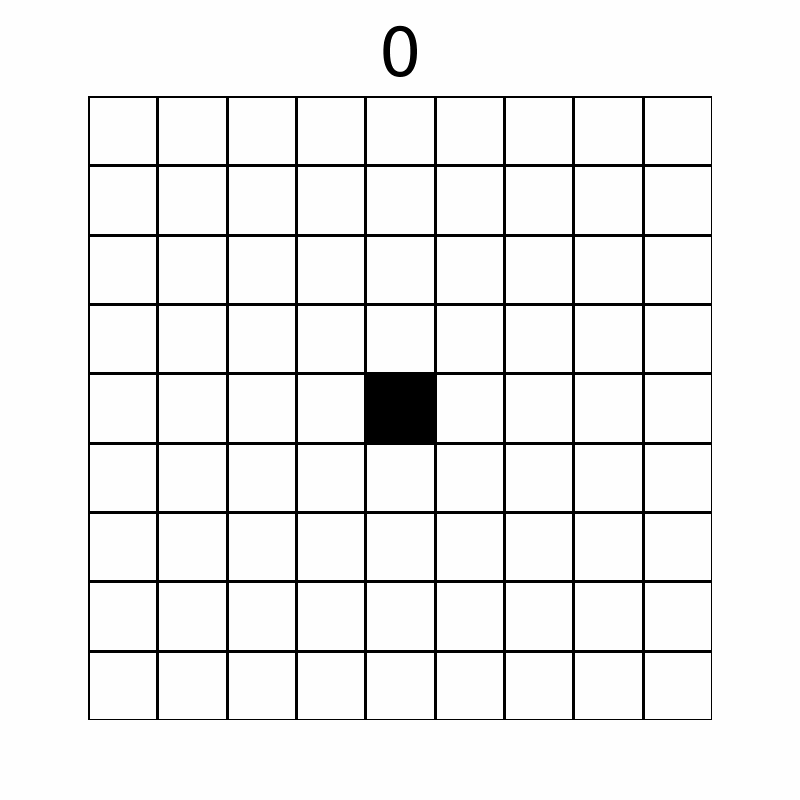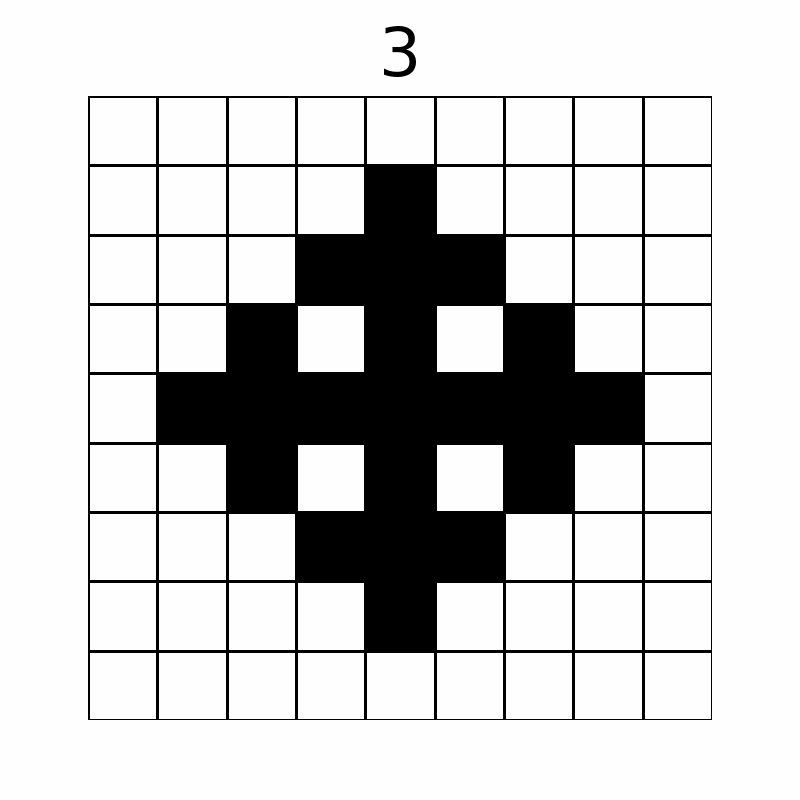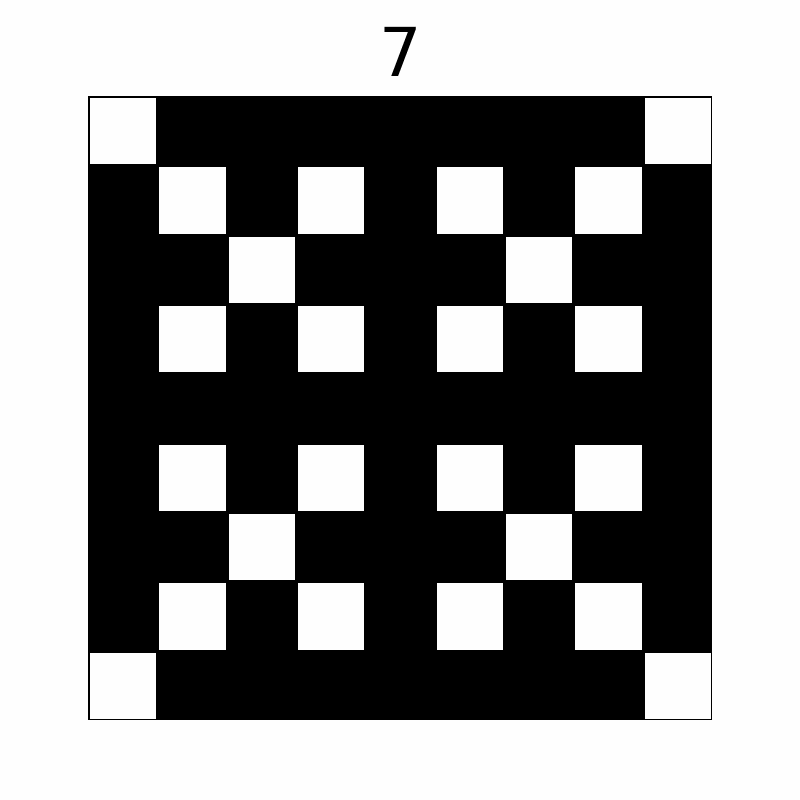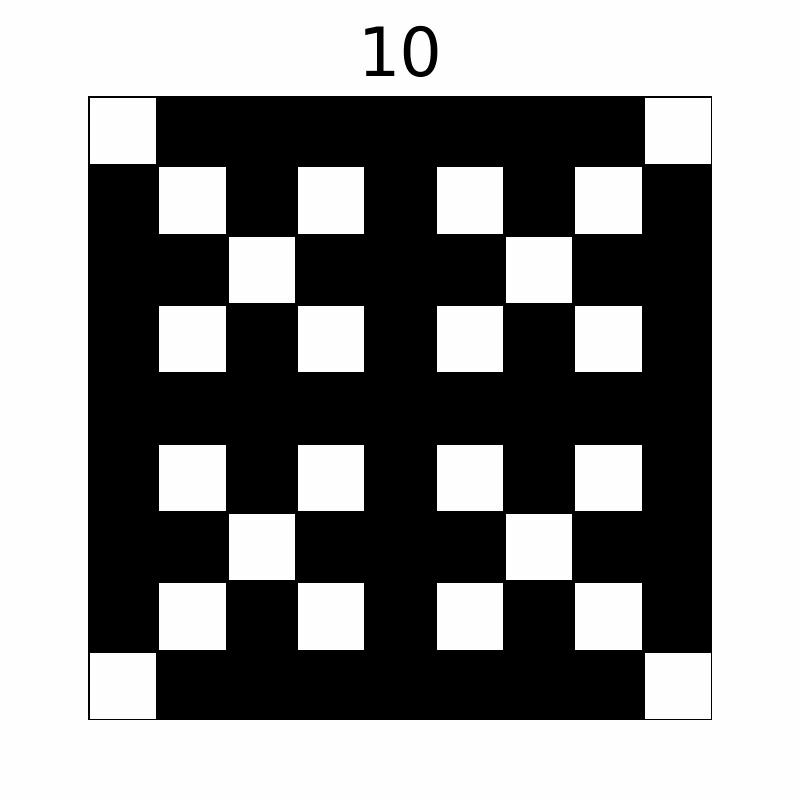
### Sample Explanation 1 操作によってマス目は以下のように変化します。（上の数字は操作回数を表しており、10 回目の操作後まで表示しています。）  最終的に黒く塗られたマスは $ 57 $ 個です。 ### Constraints - $ 2\leq H,W $ - $ HW\leq 3\times 10^5 $ - $ H,W $ は整数 - $ S_{i,j} $ は `#` または `.`