AT_abc431_e [ABC431E] Reflection on Grid

There is a grid with $ H $ rows and $ W $ columns. We will refer to the cell at the $ i $ -th row from the top and $ j $ -th column from the left as cell $ (i,j) $ . Each cell has at most one mirror placed on it. Takahashi is standing on the left side of cell $ (1,1) $ , and Aoki is standing on the right side of cell $ (H,W) $ . Takahashi has a flashlight and is shining light from the left side of cell $ (1,1) $ toward the right. Here, assume that the flashlight's light does not diffuse and is a light ray that travels straight. Takahashi's goal is to deliver the flashlight's light to Aoki by using the mirrors in the grid. There are three types of mirror placements. When light hits a mirror, the direction of the light changes according to the mirror placement. For each mirror placement, the exit direction for each entry direction is as shown in the figures below. 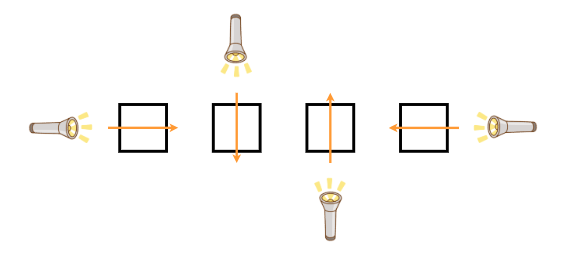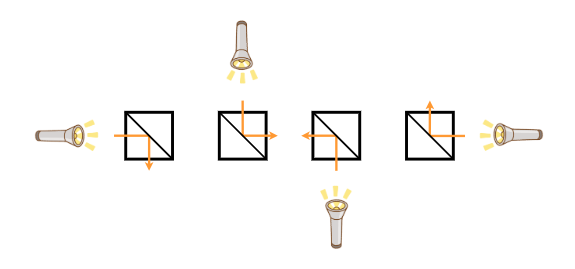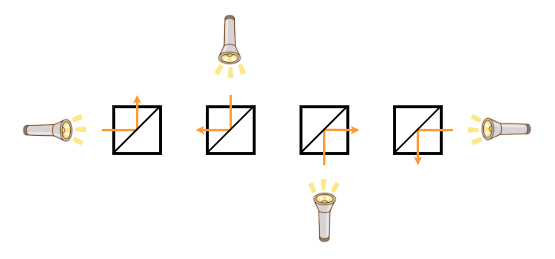- Type A (no mirror is placed)  - Type B (a mirror is placed on the diagonal connecting the upper-left and lower-right)  - Type C (a mirror is placed on the diagonal connecting the upper-right and lower-left)  The mirror placement on the grid is represented by $ H $ strings of length $ W $ : $ S_1,S_2,\ldots,S_H $ . When the $ j $ -th character of $ S_i $ is `A`, cell $ (i,j) $ is type A; when it is `B`, cell $ (i,j) $ is type B; when it is `C`, cell $ (i,j) $ is type C. Takahashi can perform the following operation any number of times to deliver the light to Aoki: - Choose one cell and change the mirror placement of that cell to a different type. Find the minimum number of operations needed to deliver the light to Aoki. You are given $ T $ test cases; find the answer for each.

The input is given from Standard Input in the following format: > $ T $ $ \mathrm{case}_1 $ $ \mathrm{case}_2 $ $ \vdots $ $ \mathrm{case}_T $ Each test case is given in the following format: > $ H $ $ W $ $ S_1 $ $ S_2 $ $ \vdots $ $ S_H $

Output $ T $ lines. The $ i $ -th line should contain the answer for the $ i $ -th test case.

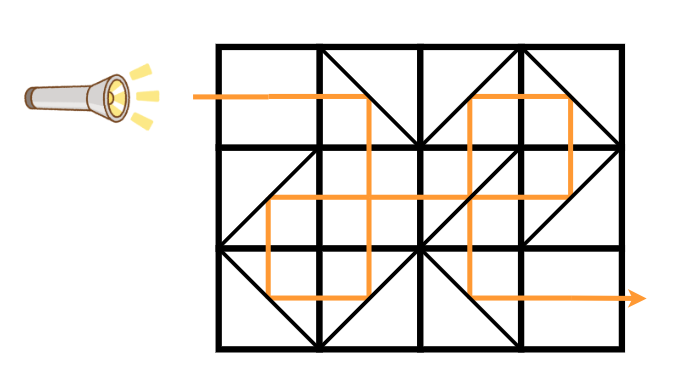
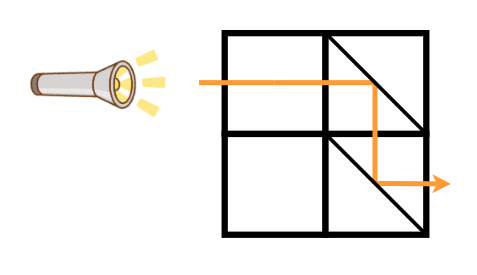
### Sample Explanation 1 For the first test case, the light can be delivered to Aoki without performing any operations.  For the second test case, by changing the mirror placement of cell $ (1,1) $ to type A and the mirror placement of cell $ (2,2) $ to type B, the light can be delivered to Aoki as shown in the figure below. It is impossible to deliver the light to Aoki with one or fewer operations, so the answer is $ 2 $ .  ### Constraints - $ 1\leq T $ - $ 1\leq H,W $ - $ HW\leq 2\times 10^5 $ - $ S_i $ is a string of length $ W $ consisting of `A`, `B`, `C`. - $ T $ , $ H $ , and $ W $ are integers. - The sum of $ HW $ over all test cases is at most $ 2\times 10^5 $ .