AT_abc431_e [ABC431E] Reflection on Grid

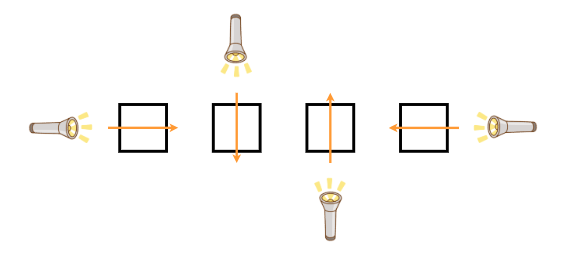
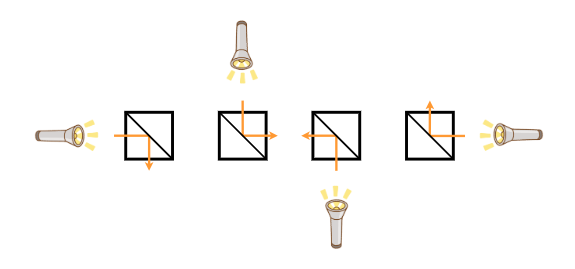
$ H $ 行 $ W $ 列のマス目があります。 上から $ i $ 行目、左から $ j $ 列目のマスをマス $ (i,j) $ と呼ぶことにします。各マスには鏡が高々 $ 1 $ 枚置いてあります。 高橋君はマス $ (1,1) $ の左側、青木くんはマス $ (H,W) $ の右側に立っています。高橋君は懐中電灯を持っており、マス $ (1,1) $ の左側から右に向かって光を入れています。ここで、懐中電灯の光は拡散せず、まっすぐに進む光線であるとします。 高橋君の目標は、マス目にある鏡を利用して懐中電灯の光を青木君に届けることです。 鏡の置き方は次の $ 3 $ 種類あります。光が鏡に当たると、鏡の置き方に応じて光の進む向きが変わります。それぞれの鏡の置き方について、光が入る方向に対する出る方向は下図のようになります。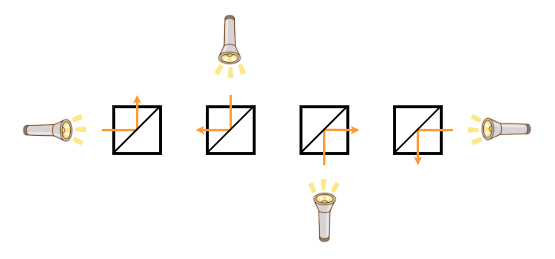 - タイプ A （鏡は置かれていない）  - タイプ B （左上と右下を結ぶ対角線上に鏡が置かれている）  - タイプ C （右上と左下を結ぶ対角線上に鏡が置かれている）  マス目の鏡の置き方は $ H $ 個の長さ $ W $ の文字列 $ S_1,S_2,\ldots,S_H $ で表されます。 $ S_i $ の $ j $ 文字目が `A` のときマス $ (i,j) $ はタイプ A、`B` のときマス $ (i,j) $ はタイプ B、`C` のときマス $ (i,j) $ はタイプ C です。 高橋君は、青木君に光を届けるために以下の操作を好きな回数行うことができます。 - あるマスを $ 1 $ つ選び、そのマスの鏡の置き方を別のタイプに変更する 青木君に光を届けるためには最低何回操作を行う必要があるか求めてください。 $ T $ 個のテストケースが与えられるので、それぞれについて答えを求めてください。

入力は以下の形式で標準入力から与えられる。 > $ T $ $ \mathrm{case}_1 $ $ \mathrm{case}_2 $ $ \vdots $ $ \mathrm{case}_T $ 各テストケースは以下の形式で与えられる。 > $ H $ $ W $ $ S_1 $ $ S_2 $ $ \vdots $ $ S_H $

$ T $ 行出力せよ。 $ i $ 行目には $ i $ 番目のテストケースに対する答えを出力せよ。

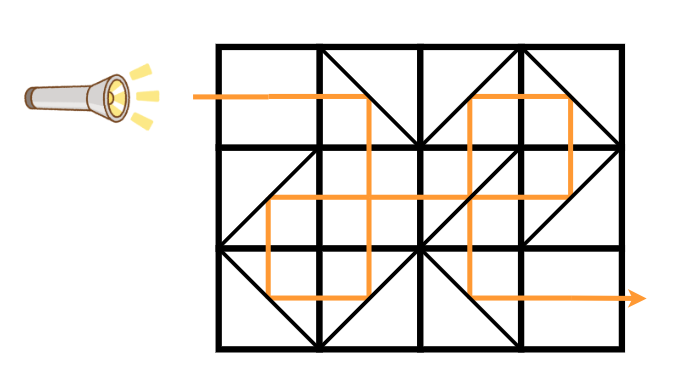
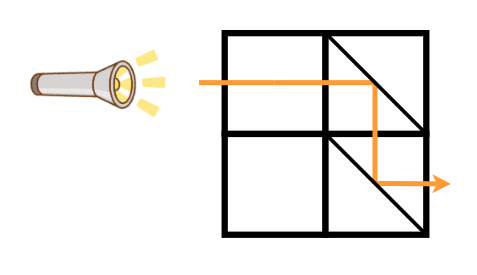
### Sample Explanation 1 $ 1 $ つ目のテストケースについて、操作を行わなくても青木君に光を届けることができます。  $ 2 $ つ目のテストケースについて、マス $ (1,1) $ の鏡の置き方をタイプ A に、マス $ (2,2) $ の鏡の置き方をタイプ B に変更することで、下図のように青木君に光を届けることができます。 $ 1 $ 回以下の操作で青木君に光を届けることはできないので、答えは $ 2 $ です。  ### Constraints - $ 1\leq T $ - $ 1\leq H,W $ - $ HW\leq 2\times 10^5 $ - $ S_i $ は `A`, `B`, `C` からなる長さ $ W $ の文字列 - $ T,H,W $ は整数 - 全てのテストケースに対する $ HW $ の総和は $ 2\times 10^5 $ 以下