AT_abc432_d [ABC432D] Suddenly, A Tempest

有一个无限大的二维网格。如果一个格子的坐标 $(x, y)$ 满足 $0 \leq x \leq X-1$ 且 $0 \leq y \leq Y-1$，那么该格子为黑色，否则为白色。 有 $N$ 场“大风暴”依次发生在该网格上。第 $i$ 场大风暴会依据字符 $C_i$ 和整数 $A_i, B_i$，按照下面的规则更新每个格子的颜色。 在第 $i$ 场大风暴中，格子 $(x, y)$ 在风暴过后颜色的更新规则如下： - 当 $C_i$ 为 `X` 时， - 若 $x < A_i$，则该格子变为风暴发生前 $(x, y + B_i)$ 的颜色； - 若 $x \geq A_i$，则该格子变为风暴发生前 $(x, y - B_i)$ 的颜色。 - 当 $C_i$ 为 `Y` 时， - 若 $y < A_i$，则该格子变为风暴发生前 $(x + B_i, y)$ 的颜色； - 若 $y \geq A_i$，则该格子变为风暴发生前 $(x - B_i, y)$ 的颜色。 若两个黑色格子 $(x_1, y_1), (x_2, y_2)$ 满足 $|x_1 - x_2| + |y_1 - y_2| = 1$，则称它们是**相邻**的。此外，如果可以通过多次移动到相邻的黑色格子，从格子 $c_1$ 走到格子 $c_2$，那么称两个黑色格子 $c_1, c_2$ 是**连通**的。 一个非空的黑色格子集合 $S$ 是一个**连通块**，当且仅当 $S$ 满足以下条件： - $S$ 内任意两格都连通； - $S$ 外的任意黑色格子都与 $S$ 内的格子不连通。 请你计算所有 $N$ 场大风暴后，网格上的连通块个数，并**按升序输出每个连通块中的格子数量**。

从标准输入读取，输入格式如下： > $N$ $X$ $Y$ $C_1$ $A_1$ $B_1$ > $\vdots$ > $C_N$ $A_N$ $B_N$

输出两行。 第一行输出黑色格子连通块的数量。 第二行按升序输出每个连通块的格子数，空格分隔。

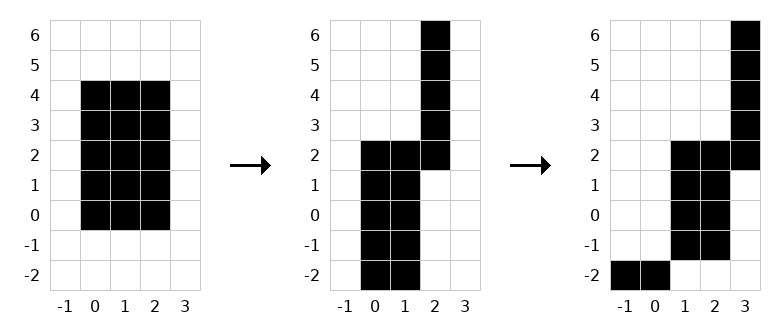
### 样例解释 1 经过多次大风暴，网格如图所示（右为 $x$ 轴正方向，上为 $y$ 轴正方向）。  最终，存在如下两个连通块： - 包含格子 $(-1, -2), (0, -2)$ 的连通块； - 包含格子 $(1,-1), (1,0), (1,1), (1,2), (2,-1), (2,0), (2,1), (2,2), (3,2), (3,3), (3,4), (3,5), (3,6)$ 的连通块。 注意，每个连通块的格子数量须按**升序**输出。 ### 样例解释 2 输出结果可能超过 32 位整数范围。 ### 数据范围 - $N, X, Y$ 是整数。 - $1 \leq N \leq 14$ - $1 \leq X,Y \leq 10^8$ - $C_i$ 为 `X` 或 `Y`。 - $A_i, B_i$ 是整数。 - $-10^8 \leq A_i, B_i \leq 10^8$。 由 ChatGPT 5 翻译