AT_abc432_d [ABC432D] Suddenly, A Tempest

There is an infinitely large two-dimensional grid. The color of cell $ (x,y) $ is black if $ 0 \leq x \leq X-1 $ and $ 0 \leq y \leq Y-1 $ , and white otherwise. $ N $ great storms occur in order on this grid. The $ i $ -th great storm updates the color of each cell on the grid according to a rule represented by a character $ C_i $ and integers $ A_i, B_i $ . In the $ i $ -th great storm, the color of cell $ (x, y) $ after the great storm is: - In case $ C_i $ is `X`, - if $ x < A_i $ , it becomes the color of cell $ (x, y + B_i) $ before the great storm; - if $ x \geq A_i $ , it becomes the color of cell $ (x, y - B_i) $ before the great storm. - In case $ C_i $ is `Y`, - if $ y < A_i $ , it becomes the color of cell $ (x + B_i, y) $ before the great storm; - if $ y \geq A_i $ , it becomes the color of cell $ (x - B_i, y) $ before the great storm. Two black cells $ (x_1, y_1), (x_2, y_2) $ are **adjacent** if and only if $ |x_1 - x_2| + |y_1 - y_2| = 1 $ . Also, two black cells $ c_1, c_2 $ are **connected** if and only if one can move from cell $ c_1 $ to cell $ c_2 $ by repeatedly moving to adjacent black cells. A non-empty set $ S $ of black cells is a **connected component** if and only if $ S $ satisfies the following conditions: - Any two cells in $ S $ are connected. - Every black cell not in $ S $ is not connected to any cell in $ S $ . For the grid after all $ N $ great storms have occurred, find the number of connected components and output the number of cells in each connected component **in ascending order**.

The input is given from Standard Input in the following format: > $ N $ $ X $ $ Y $ $ C_1 $ $ A_1 $ $ B_1 $ $ \vdots $ $ C_N $ $ A_N $ $ B_N $

Output two lines. The first line should contain the number of connected components consisting of black cells. The second line should contain the number of cells in each connected component, space-separated, **in ascending order**.

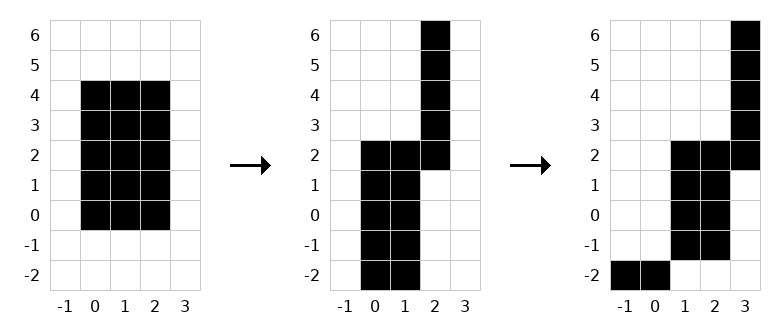
### Sample Explanation 1 The grid changes as shown in the following image due to the great storms (the rightward direction is the positive direction of the $ x $ -axis, and the upward direction is the positive direction of the $ y $ -axis).  In the final grid, the following two connected components exist: - A connected component consisting of cells $ (-1,-2), (0,-2) $ . - A connected component consisting of cells $ (1,-1), (1,0), (1,1), (1,2), (2,-1), (2,0), (2,1), (2,2), (3,2), (3,3), (3,4), (3,5), (3,6) $ . Note that the number of cells in each connected component must be output **in ascending order**. ### Sample Explanation 2 The output value may not fit in a 32-bit integer. ### Constraints - $ N, X, Y $ are integers. - $ 1 \leq N \leq 14 $ - $ 1 \leq X,Y \leq 10^8 $ - $ C_i $ is `X` or `Y`. - $ A_i, B_i $ are integers. - $ -10^8 \leq A_i, B_i \leq 10^8 $