AT_abc432_d [ABC432D] Suddenly, A Tempest

無限に広がる二次元グリッドがあります。マス $ (x,y) $ の色は、 $ 0 \leq x \leq X-1 $ かつ $ 0 \leq y \leq Y-1 $ ならば黒であり、そうでなければ白です。 このグリッドに対して $ N $ 個の大嵐が順に発生します。 $ i $ 回目の大嵐は、文字 $ C_i $ と整数 $ A_i, B_i $ で表される法則にしたがって、グリッド上の各マスの色を更新します。 $ i $ 回目の大嵐において、大嵐が起きた後のマス $ (x, y) $ の色は、 - $ C_i $ が `X` の場合、 - $ x < A_i $ ならば、大嵐が起きる前のマス $ (x, y + B_i) $ の色になる。 - $ x \geq A_i $ ならば、大嵐が起きる前のマス $ (x, y - B_i) $ の色になる。 - $ C_i $ が `Y` の場合、 - $ y < A_i $ ならば、大嵐が起きる前のマス $ (x + B_i, y) $ の色になる。 - $ y \geq A_i $ ならば、大嵐が起きる前のマス $ (x - B_i, y) $ の色になる。 $ 2 $ つの黒いマス $ (x_1, y_1), (x_2, y_2) $ が**隣接している**とは、 $ |x_1 - x_2| + |y_1 - y_2| = 1 $ が満たされることを指します。また、 $ 2 $ つの黒いマス $ c_1, c_2 $ が**連結である**とは、隣接する黒いマスへの移動を繰り返すことでマス $ c_1 $ からマス $ c_2 $ に移動できることを指します。 空でない黒いマスの集合 $ S $ が**連結成分**であるとは、 $ S $ が以下の条件を満たすことを指します。 - $ S $ に属するどの $ 2 $ マスも連結である。 - $ S $ に属さないすべての黒いマスが、 $ S $ に属するどのマスとも連結でない。 $ N $ 個の大嵐がすべて発生した後のグリッドについて、連結成分の個数を求め、各連結成分におけるマスの個数を**昇順に**出力してください。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ X $ $ Y $ $ C_1 $ $ A_1 $ $ B_1 $ $ \vdots $ $ C_N $ $ A_N $ $ B_N $

$ 2 $ 行出力せよ。 $ 1 $ 行目には、黒いマスからなる連結成分の個数を出力せよ。 $ 2 $ 行目には、各連結成分におけるマスの個数を、空白区切りで**昇順に**出力せよ。

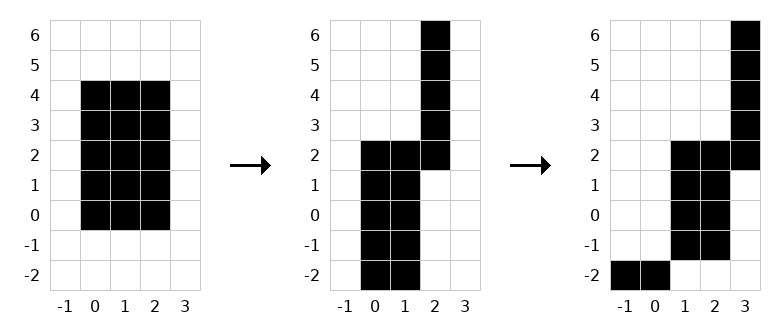
### Sample Explanation 1 大嵐によって、グリッドは以下の画像のように変化します(右方向が $ x $ 軸の正の向き、上方向が $ y $ 軸の正の向き)。  最終的なグリッドにおいて、以下の $ 2 $ つの連結成分が存在します。 - マス $ (-1,-2), (0,-2) $ からなる連結成分。 - マス $ (1,-1), (1,0), (1,1), (1,2), (2,-1), (2,0), (2,1), (2,2), (3,2), (3,3), (3,4), (3,5), (3,6) $ からなる連結成分。 各連結成分がもつマスの個数は**昇順に**出力する必要があることに注意してください。 ### Sample Explanation 2 出力する値は 32bit 整数に収まらないことがあります。 ### Constraints - $ N, X, Y $ は整数 - $ 1 \leq N \leq 14 $ - $ 1 \leq X,Y \leq 10^8 $ - $ C_i $ は `X` または `Y` - $ A_i, B_i $ は整数 - $ -10^8 \leq A_i, B_i \leq 10^8 $