AT_abc434_d [ABC434D] Clouds

The sky is represented by a $ 2000 \times 2000 $ grid. When looking up at the sky, the cell at the $ r $ -th row from the top and $ c $ -th column from the left is called $ (r,c) $ . Currently, there are clouds $ 1,2,\dots,N $ floating in this sky. The cell $ (r,c) $ is covered by cloud $ i $ if and only if it satisfies $ U_i \le r \le D_i $ and $ L_i \le c \le R_i $ . For $ k=1,2,\dots,N $ , answer the following question: - Remove only cloud $ k $ from the $ N $ clouds. At this point, there are $ N-1 $ clouds floating in the sky. How many cells are not covered by any cloud?

The input is given from Standard Input in the following format: > $ N $ $ U_1 $ $ D_1 $ $ L_1 $ $ R_1 $ $ U_2 $ $ D_2 $ $ L_2 $ $ R_2 $ $ \vdots $ $ U_N $ $ D_N $ $ L_N $ $ R_N $

Output $ N $ lines. The $ i $ -th line should contain the answer to the question when $ k=i $ .

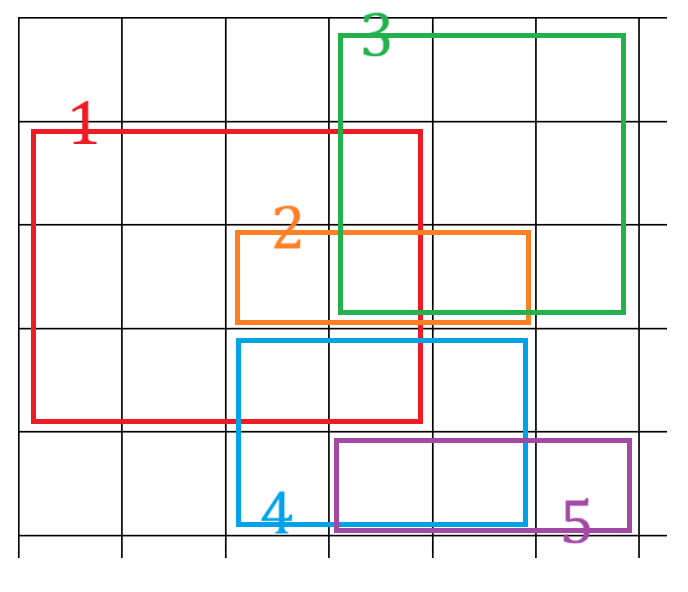
### Sample Explanation 1 The figure shows the top-left $ 5 \times 6 $ region of the sky.  - When cloud $ 1 $ is removed, the number of cells covered by some cloud is $ 17 $ , so the number of cells not covered by any cloud is $ 3999983 $ . - When cloud $ 2 $ is removed, the number of cells covered by some cloud is $ 24 $ , so the number of cells not covered by any cloud is $ 3999976 $ . - When cloud $ 3 $ is removed, the number of cells covered by some cloud is $ 18 $ , so the number of cells not covered by any cloud is $ 3999982 $ . - When cloud $ 4 $ is removed, the number of cells covered by some cloud is $ 22 $ , so the number of cells not covered by any cloud is $ 3999978 $ . - When cloud $ 5 $ is removed, the number of cells covered by some cloud is $ 23 $ , so the number of cells not covered by any cloud is $ 3999977 $ . ### Constraints - $ 1 \le N \le 2 \times 10^5 $ - $ 1 \le U_i \le D_i \le 2000 $ - $ 1 \le L_i \le R_i \le 2000 $ - All input values are integers.