AT_abc435_d [ABC435D] Reachability Query 2

给你一个有向图，包含 $N$ 个顶点和 $M$ 条边。 顶点编号为 $1$ 到 $N$，第 $i$ 条边是从顶点 $X_i$ 指向顶点 $Y_i$ 的有向边。 初始时，所有顶点都是白色。 请依次处理 $Q$ 个查询。每个查询有如下两种类型之一： - `1 v`：将顶点 $v$ 染成黑色。 - `2 v`：判断是否存在一条路径，可以从顶点 $v$ 沿边行走到某个黑色顶点。

输入从标准输入读取，格式如下： > $N\ M$ > $X_1\ Y_1$ > $\vdots$ > $X_M\ Y_M$ > $Q$ > $\mathrm{query}_1$ > $\vdots$ > $\mathrm{query}_Q$ $\mathrm{query}_i$ 表示第 $i$ 个查询，具体格式如下： > $1\ v$ 或 > $2\ v$

设共有 $q$ 个第二种类型的查询。输出 $q$ 行。 对于第 $i$ 个第二种类型的查询，如果能够从顶点 $v$ 沿边到达某个黑色顶点，输出 `Yes`，否则输出 `No`。

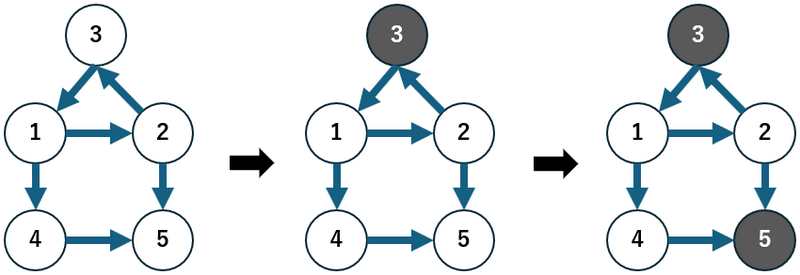
### 样例解释 1 - 初始时，给定图如下最左侧图所示。 - 第一个查询后，顶点 $3$ 被染成黑色，如中间所示。 - 对第二个查询，可以从顶点 $1$ 沿路径到达黑色顶点 $3$。 - 第三个查询，从顶点 $4$ 无法到达任何黑色顶点。 - 第四个查询后，顶点 $5$ 被染成黑色，如最右侧所示。 - 第五个查询，从顶点 $4$ 开始可以到达黑色顶点 $5$。  ### 数据范围 - $1 \leq N \leq 3 \times 10^5$ - $0 \leq M \leq 3 \times 10^5$ - $1 \leq Q \leq 3 \times 10^5$ - $1 \leq X_i, Y_i \leq N$ - 不存在自环，即 $X_i \neq Y_i$。 - 不存在重边，即 $(X_i, Y_i)$ 互不相同。 - 查询中的 $1 \leq v \leq N$。 - 所有输入均为整数。 由 ChatGPT 5 翻译