AT_abc435_d [ABC435D] Reachability Query 2

You are given a directed graph with $ N $ vertices and $ M $ edges. The vertices are numbered from $ 1 $ to $ N $ , and the $ i $ -th edge is a directed edge from vertex $ X_i $ to vertex $ Y_i $ . Initially, all vertices are white. Process $ Q $ queries in order. Each query is of one of the following two types: - `1 v`: Color vertex $ v $ black. - `2 v`: Determine whether it is possible to reach a black vertex by following edges from vertex $ v $ .

The input is given from Standard Input in the following format: > $ N $ $ M $ $ X_1 $ $ Y_1 $ $ \vdots $ $ X_M $ $ Y_M $ $ Q $ $ \mathrm{query}_1 $ $ \vdots $ $ \mathrm{query}_Q $ $ \mathrm{query}_i $ represents the $ i $ -th query and is given in one of the following formats: > $ 1 $ $ v $ > $ 2 $ $ v $

Let $ q $ be the number of queries of the second type. Output $ q $ lines. The $ i $ -th line should contain `Yes` if a black vertex is reachable in the $ i $ -th query of the second type, and `No` otherwise.

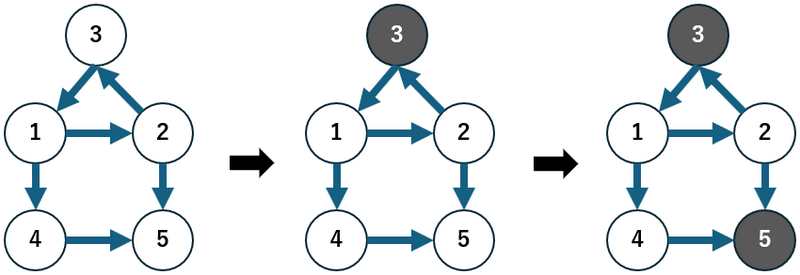
### Sample Explanation 1 - Initially, the given graph is as shown in the leftmost figure below. - By the first query, vertex $ 3 $ becomes black, as shown in the center figure. - In the second query, it is possible to reach black vertex $ 3 $ from vertex $ 1 $ . - In the third query, it is not possible to reach a black vertex from vertex $ 4 $ . - By the fourth query, vertex $ 5 $ becomes black, as shown in the rightmost figure. - In the fifth query, it is possible to reach black vertex $ 5 $ from vertex $ 4 $ .  ### Constraints - $ 1\leq N \leq 3\times 10^5 $ - $ 0\leq M \leq 3\times 10^5 $ - $ 1\leq Q \leq 3\times 10^5 $ - $ 1\leq X_i,Y_i \leq N $ - There are no self-loops, that is, $ X_i \neq Y_i $ . - There are no multiple edges, that is, $ (X_i,Y_i) $ are distinct. - In queries, $ 1 \leq v \leq N $ . - All input values are integers.