AT_abc435_g [ABC435G] Domino Arrangement

有 $N$ 个格子，编号为 $1$ 到 $N$。最初，所有格子都没有被涂色。 有 $M$ 种颜色，第 $i$ 种颜色可以用来涂色区间 $L_i,L_i+1,\ldots,R_i$ 中的任意多个格子。 请计算满足下列条件的涂色方案数，对 $998244353$ 取模： - 对于每个格子 $i$，如果该格子被涂某种颜色，则在格子 $i-1$ 和格子 $i+1$ 中，恰好有一个格子被涂上与 $i$ 相同的颜色。 - 这里，认为格子 $0$ 和格子 $N+1$ 都没有被涂色。

输入从标准输入中给出，格式如下： > $N$ $M$ > $L_1$ $R_1$ > ⋮ > $L_M$ $R_M$

输出答案。

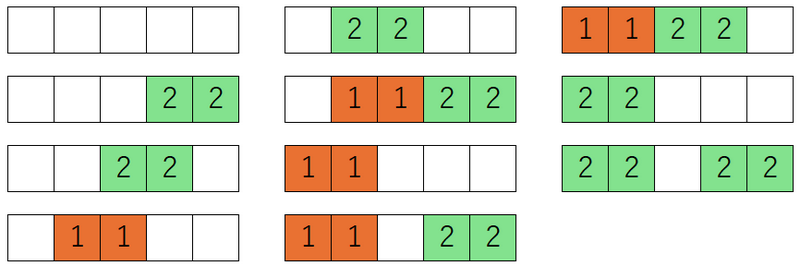
### 样例解释 1 第一种颜色可以涂色格子 $1,2,3$，第二种颜色可以涂色格子 $1,2,3,4,5$。 共有 $11$ 种满足条件的方案，如下图所示：  ### 样例解释 2 所有格子都不涂色也满足条件。 ### 样例解释 3 请对 $998244353$ 取模。 ### 数据范围 - $1\leq N,M \leq 5\times 10^5$ - $1\leq L_i \leq R_i \leq N$ - 所有输入均为整数。 由 ChatGPT 5 翻译