AT_abc435_g [ABC435G] Domino Arrangement

There are $ N $ cells numbered from $ 1 $ to $ N $ . Initially, no cell is painted with any color. There are $ M $ types of colors, and with the $ i $ -th color, you can paint any number of cells you like among cells $ L_i,L_i+1,\ldots,R_i $ . Find the number, modulo $ 998244353 $ , of ways to paint the cells that satisfy the following condition: - For every cell $ i $ , if that cell is painted with a color, then exactly one of cells $ i-1 $ and $ i+1 $ is painted with the same color as cell $ i $ . - Here, cells $ 0 $ and $ N+1 $ are considered to be not painted with any color.

The input is given from Standard Input in the following format: > $ N $ $ M $ $ L_1 $ $ R_1 $ $ \vdots $ $ L_M $ $ R_M $

Output the answer.

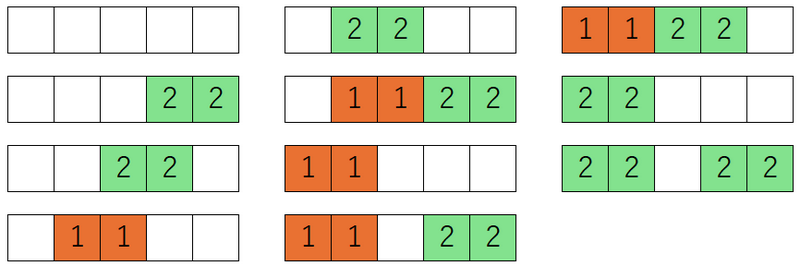
### Sample Explanation 1 The first color can paint cells $ 1,2,3 $ , and the second color can paint cells $ 1,2,3,4,5 $ . There are $ 11 $ ways to paint that satisfy the condition, as follows:  ### Sample Explanation 2 The one way of not painting any cell satisfies the condition. ### Sample Explanation 3 Find the count modulo $ 998244353 $ . ### Constraints - $ 1\leq N,M \leq 5\times 10^5 $ - $ 1\leq L_i \leq R_i \leq N $ - All input values are integers.