AT_abc441_g [ABC441G] Takoyaki and Flip

$ N $ 枚の皿が左から右に一直線状に並んでいます。 左から $ i $ 番目 $ (1\le i\le N) $ の皿を皿 $ i $ と呼ぶことにします。 はじめ、どの皿も表を上にして置かれており、どの皿にもたこ焼きが置かれていません。 次の $ 3 $ 種類のクエリを合計 $ Q $ 回処理してください。 - タイプ $ 1 $ ：整数 $ L,R,X $ が与えられる。 $ i=L,L+1,\ldots,R $ に対して、皿 $ i $ が表を上にして置かれているなら、皿 $ i $ にたこ焼きを $ X $ 個置く。 - タイプ $ 2 $ ：整数 $ L,R $ が与えられる。 $ i=L,L+1,\ldots,R $ に対して、皿 $ i $ にたこ焼きが $ 1 $ 個以上置かれていた場合、皿 $ i $ に置かれているたこ焼きをすべて食べる。皿 $ i $ をひっくり返す（皿が表を上にして置かれている場合裏を上にして置き、そうでない場合表を上にして置く）。 - タイプ $ 3 $ ：整数 $ L,R $ が与えられる。皿 $ L, $ 皿 $ L+1,\ldots, $ 皿 $ R $ にわたる、置かれているたこ焼きの個数の最大値を出力する。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ Q $ $ \mathrm{query} _ 1 $ $ \mathrm{query} _ 2 $ $ \vdots $ $ \mathrm{query} _ Q $ ここで、 $ \mathrm{query} _ i $ は $ i $ 番目 $ (1\le i\le Q) $ のクエリを表し、次のどちらかの形式で与えられる。 > $ t $ $ L $ $ R $ $ X $ > $ t $ $ L $ $ R $ これらは、 $ i $ 番目のクエリがタイプ $ t $ のクエリで、与えられる整数が $ L,R,X $ もしくは $ L,R $ であることを表す。 タイプ $ 1 $ のクエリは前者の形式で、それ以外のクエリは後者の形式で与えられる。

タイプ $ 3 $ のクエリの個数を $ q $ として、 $ q $ 行にわたって出力せよ。 $ i $ 行目 $ (1\le i\le q) $ には、タイプ $ 3 $ のクエリのうち先頭から $ i $ 番目のものに対する答えを出力せよ。

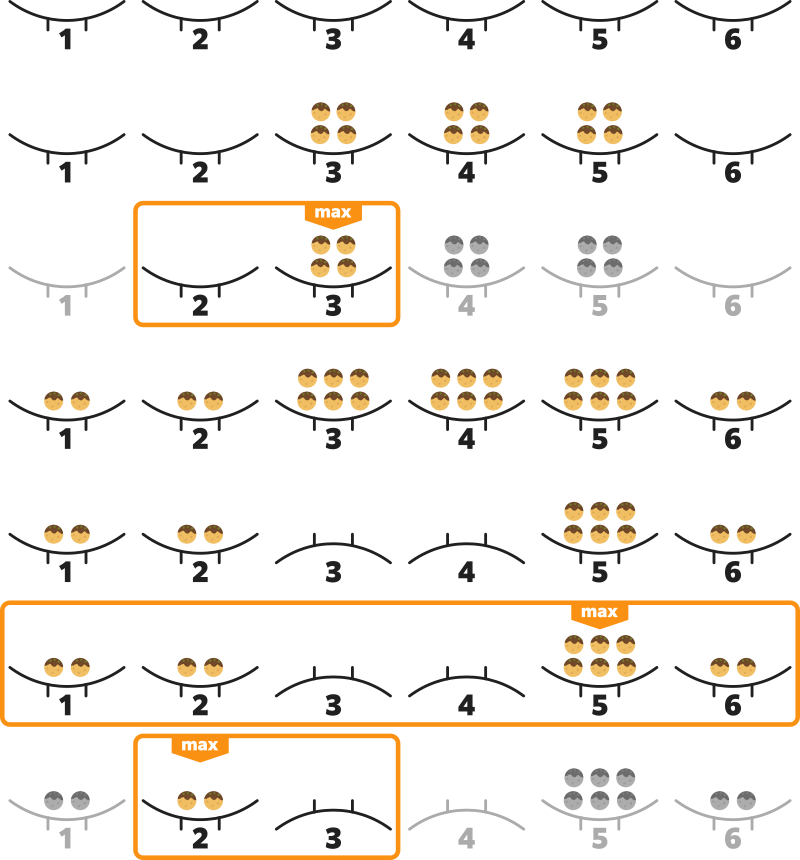
### Sample Explanation 1 各クエリの時点で、それぞれの皿の状態とその上に置かれているたこ焼きの個数は以下の図のようになります。  $ 2 $ 番目のクエリの時点では、皿 $ 2 $ と皿 $ 3 $ のうち置かれているたこ焼きの個数がより多いのは皿 $ 3 $ です。 よって、 $ 1 $ 行目には皿 $ 3 $ に置かれているたこ焼きの個数である `4` を出力してください。 $ 5 $ 番目のクエリの時点では、皿 $ 1, $ 皿 $ 2,\ldots, $ 皿 $ 6 $ のうち置かれているたこ焼きの個数が最も多いのは皿 $ 5 $ です。 よって、 $ 2 $ 行目には皿 $ 5 $ に置かれているたこ焼きの個数である `6` を出力してください。 $ 6 $ 番目のクエリの時点では、皿 $ 2 $ と皿 $ 3 $ のうち置かれているたこ焼きの個数がより多いのは皿 $ 2 $ です。 よって、 $ 3 $ 行目には皿 $ 2 $ に置かれているたこ焼きの個数である `2` を出力してください。 ### Sample Explanation 2 裏を上にして置かれている皿にはひとつもたこ焼きは置かれないことに注意してください。 また、答えが $ 2 ^ {32} $ 以上になる場合があることに注意してください。 ### Constraints - $ 1\le N\le2\times10 ^ 5 $ - $ 1\le Q\le2\times10 ^ 5 $ - すべてのクエリにおいて、 $ 1\le L\le R\le N $ - タイプ $ 1 $ のクエリにおいて、 $ 1\le X\le10 ^ 9 $ - タイプ $ 3 $ のクエリが存在する。 - 入力はすべて整数