AT_abc442_e [ABC442E] Laser Takahashi

There are $ N $ monsters on a two-dimensional plane. The monsters are numbered from $ 1 $ to $ N $ , and the coordinates of monster $ i $ are $ (X_i,Y_i) $ . Here, $ (X_i,Y_i) \neq (0,0) $ . (Each monster can be regarded as a stationary point. That is, monsters have no size.) Takahashi is standing at the origin of this plane. A powerful laser is always emitted from his eyes, instantly destroying monsters in the direction he is facing. If multiple monsters exist in the direction he is facing, all of them are instantly destroyed. Aoki is conducting $ Q $ **independent** thought experiments. The $ j $ -th thought experiment is as follows: - Initially, Takahashi is facing the direction toward monster $ A_j $ . From now on, Takahashi will rotate **clockwise** and stop the moment he faces the direction toward monster $ B_j $ . Here, how many monsters in total (including monsters $ A_j $ and $ B_j $ ) will be destroyed? If monsters $ A_j $ and $ B_j $ exist in the same direction from the origin, Takahashi does not rotate at all. Find the answer to each thought experiment.

The input is given from Standard Input in the following format: > $ N $ $ Q $ $ X_1 $ $ Y_1 $ $ X_2 $ $ Y_2 $ $ \vdots $ $ X_N $ $ Y_N $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ $ \vdots $ $ A_Q $ $ B_Q $

Output $ Q $ lines. The $ j $ -th line $ (1\leq j \leq Q) $ should contain the answer to the $ j $ -th thought experiment.

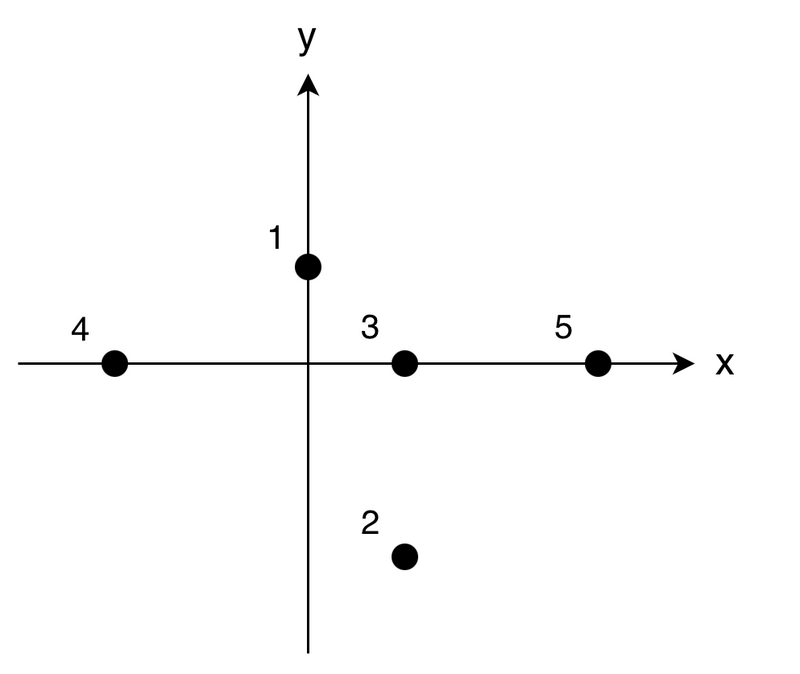
### Sample Explanation 1  - $ 1 $ -st thought experiment: Initially, Takahashi is facing the direction toward monster $ 4 $ (at this time, monster $ 4 $ is destroyed). From here, he continues to rotate clockwise and stops the moment he faces the direction toward monster $ 1 $ (at this time, monster $ 1 $ is destroyed). Since he does not face the direction toward any other monsters, the answer is $ 2 $ . - $ 2 $ -nd thought experiment: Initially, Takahashi is facing the direction toward monster $ 1 $ (at this time, monster $ 1 $ is destroyed). From here, as he continues to rotate clockwise, he faces the direction toward monsters $ 3 $ and $ 5 $ along the way, so they are destroyed. As he continues to rotate further, he faces the direction toward monster $ 2 $ along the way, so it is destroyed. Finally, he stops the moment he faces the direction toward monster $ 4 $ (at this time, monster $ 4 $ is destroyed). Therefore, the answer is $ 5 $ . - $ 3 $ -rd thought experiment: Monsters $ 3, 5, 2, 4 $ are destroyed, so the answer is $ 4 $ . - $ 4 $ -th thought experiment: Monsters $ 3, 5 $ are destroyed, so the answer is $ 2 $ . Note that since monsters $ 3 $ and $ 5 $ exist in the same direction from the origin, Takahashi does not rotate at all. ### Sample Explanation 2 Multiple monsters may exist at the same coordinates. ### Constraints - $ 2\leq N \leq 2\times 10^5 $ - $ 1\leq Q \leq 2\times 10^5 $ - $ -10^9\leq X_i,Y_i \leq 10^9 $ - $ (X_i,Y_i)\neq (0,0) $ - $ 1\leq A_j,B_j\leq N $ - $ A_j\neq B_j $ - All input values are integers.