AT_agc004_c [AGC004C] AND Grid

高桥君和青木君各自获得了一张 $H$ 行 $W$ 列的透明方格纸。 高桥君将自己方格纸的一部分格子涂成了红色。此时，红色格子是上下左右四连通的。也就是说，从任意红色格子出发，仅通过上下左右相邻的红色格子即可到达其他任意红色格子。 同样，青木君将自己方格纸的一部分格子涂成了蓝色。此时，蓝色格子也是上下左右四连通的。 之后，高桥君和青木君将两张方格纸按原方向完全重叠。于是，只有红色格子和蓝色格子重叠的格子呈现为紫色。 紫色格子的布局以字符 $a_{i,j}$ ($1 \leq i \leq H $，$ 1 \leq j \leq W$) 组成的矩形形式给出，表示从上往下第 $i$ 行、从左往右第 $j$ 列的格子如果是紫色，则 $a_{i,j}$ 为 `#`；如果不是紫色，则 $a_{i,j}$ 为 `.`。**保证最外圈的格子不是紫色**。也就是说，当 $i=1, H$ 或 $j=1, W$ 时，保证 $a_{ij}$ 为 `.`。 请找出满足题目条件的一组红色格子布局和蓝色格子布局的组合。可以证明解一定存在。

第一行两个整数 $H$，$W$，表示方格纸的行数和列数。 接下来 $H$ 行，每行 $W$ 个整数，输入数据的第 $(i+1)$ 行第 $j$ 列表示重叠后所得方格纸的格子 $a_{i,j}$。

输出满足题目条件的一组红色格子布局和蓝色格子布局的组合。 - 第 $1$ 行到第 $H$ 行输出红色格子的布局。 - 第 $H+1$ 行输出一个空行。 - 第 $H+2$ 行到第 $2H+1$ 行输出蓝色格子的布局。 两者的输出格式应与紫色格子布局的格式相同。

### 数据范围 - $3 \leq H, W \leq 500$ - 保证 $a_{ij}$ 是 `#` 或 `.`。 - 保证当 $i=1, H$ 或 $j=1, W$ 时，$a_{i,j}$ 是 `.`。 - 保证 $a_{i,j}$ 中至少有一个 `#`。 ### 样例解释 #1 例如，可以考虑以下红色格子布局和蓝色格子布局的组合。 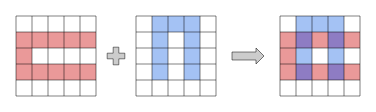 ### 样例解释 #2 例如，可以考虑以下红色格子布局和蓝色格子布局的组合。