AT_agc007_c [AGC007C] Pushing Balls

有 $N$ 个球和 $N+1$ 个洞沿一条直线排列。球从左到右依次编号为 $1$ 到 $N$，洞从左到右依次编号为 $1$ 到 $N+1$。第 $i$ 个球被放置在第 $i$ 个洞和第 $i+1$ 个洞之间。将相邻的洞和球之间的距离从左到右依次记为数列 $d_i$（$1 \leq i \leq 2N$）。已知 $d_1$ 的值和参数 $x$，并且对于任意 $i$（$2 \leq i \leq 2N$），都有 $d_i - d_{i-1} = x$。 现在考虑将这 $N$ 个球依次滚动，使其掉入洞中。球经过某个洞上方时，如果该洞还没有其他球落入，则球会掉入该洞；如果该洞已经有球，则球不会掉入，继续滚动。（在本题的滚动方式下，球之间不会发生碰撞。） 每次滚动时，从尚未滚动的球中等概率随机选择一个球，并以等概率向左或向右滚动。重复 $N$ 次，直到所有球都被滚动。请计算所有球移动距离总和的期望值。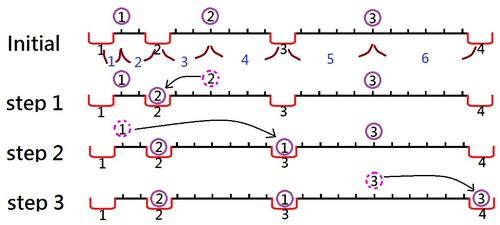 以下是 $N=3$，$d_1=1$，$x=1$ 时的一个滚动示例：  1. 将第 $2$ 个球向左滚动。球会掉入第 $2$ 个洞，移动距离为 $3$。 2. 将第 $1$ 个球向右滚动。球会经过第 $2$ 个洞上方，最终掉入第 $3$ 个洞，移动距离为 $9$。 3. 将第 $3$ 个球向右滚动。球会掉入第 $4$ 个洞，移动距离为 $6$。 在这个例子中，所有球移动距离的总和为 $18$。 无论如何滚动，所有球最终都会掉入某个洞，最后会剩下一个空洞。

输入为一行，包含三个整数： > $N$ $d_1$ $x$

输出答案，要求为小数。绝对误差或相对误差需在 $10^{-9}$ 以内。

## 限制 - $1 \leq N \leq 200,\!000$ - $1 \leq d_1 \leq 100$ - $0 \leq x \leq 100$ - 所有输入值均为整数。 ## 样例解释 1 有 $1$ 个球，$2$ 个洞。球到左侧洞的距离为 $3$，到右侧洞的距离为 $6$。球可以向左或向右滚动，共 $2$ 种方式，移动距离分别为 $3,\ 6$。因此答案为 $(3+6)/2 = 4.5$。 由 ChatGPT 4.1 翻译