AT_agc011_c [AGC011C] Squared Graph

高桥君得到了一个包含 $N$ 个顶点 $1,2,\ldots,N$ 的无向图。图的每条边表示为 $(u_i, v_i)$。该图中不存在自环或重边。 高桥君决定以这个图为基础，构建一个包含 $N^2$ 个顶点 $(a, b)$（$1 \leq a \leq N, 1 \leq b \leq N$）的新图。新图中的边按如下规则确定： - 当且仅当原图中 $a$ 与 $a'$ 之间有一条边，且 $b$ 与 $b'$ 之间也有一条边时，在新图中的 $(a, b)$ 与 $(a', b')$ 之间连一条边。 请你求出高桥君构建的新图中的连通分量个数。

输入以如下格式从标准输入给出。 > $N$ $M$ $u_1$ $v_1$ $u_2$ $v_2$ … $u_M$ $v_M$

输出高桥君构建的新图中的连通分量个数。

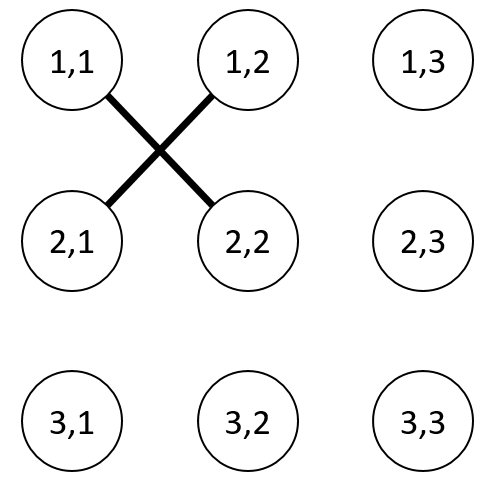
## 限制条件 - $2 \leq N \leq 100,\!000$ - $0 \leq M \leq 200,\!000$ - $1 \leq u_i < v_i \leq N$ - 不存在满足 $u_i = u_j$ 且 $v_i = v_j$ 的不同 $i, j$ 的组 ## 样例解释 1 高桥君构建的新图如下图所示。  由 ChatGPT 5 翻译