AT_agc011_f [AGC011F] Train Service Planning

在高桥王国中有一条铁路，这条铁路分为 $N$ 个区间，标号为 $1, 2, \dots, N$，有 $N+1$ 个站台，标号为 $0, 1, \dots, N$，区间 $i$ 连接站台 $i-1$ 和站台 $i$，一列火车经过区间 $i$ 会消耗 $A_i$ 的时间，每个区间的铁路要么是单向通行的，要么是双向通行的，$B_i=1$ 表示区间 $i$ 是单向通行的，否则它是双向通行的。对于两列相向而行的火车，且它们行驶在一段铁轨上，如果这个铁轨是双向的，那么两列火车可以跨过在这段铁轨穿过对方继续行驶。对于一列停靠在站台的火车，任意一列火车都可以穿过对方继续行驶。 现在 snuke 君想要设计一个火车时间表，即需要对所有车站设定所有列车的到达和离开时间，满足以下约定： - 所有的火车要么从站台 $0$ 到站台 $N$，要么从站台 $N$ 到站台 $0$； - 对任意一列火车，它通过区间 $i$ 的时间必须为 $A_i$; - 对任意一列终点为站台 $N$ 的火车，如果它在 $s$ 时刻到达站台 $i$ 并在 $t$ 时刻离开站台 $i$，那么下一列经过站台 $i$ 的终点为站台 $N$ 的火车必须在 $s+K$ 时刻到达站台 $i$ 并在 $t+K$ 时刻离开站台 $i$，同理，上一列经过站台 $i$ 的终点为站台 $N$ 的火车必须在 $s-K$ 时刻到达站台 $i$ 并在 $t-K$ 时刻离开站台 $i$，对于终点为站台 $0$ 的火车也必须如此； - 在任意时刻不能有两列相向而行的火车在单向区间内互相穿过。 现在你要找出一个时间表，使得一列从站台 $0$ 到站台 $N$ 的火车和一列从站台 $N$ 到站台 $0$ 的火车行驶时间之和最短，观察样例 $1$ 可以帮助你更好地理解题目。

$ N $ $ K $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ : $ A_N $ $ B_N $

一行一个整数，表示列车上下行最短的开车时间之和，如果不存在合法方案则输出 $-1$。

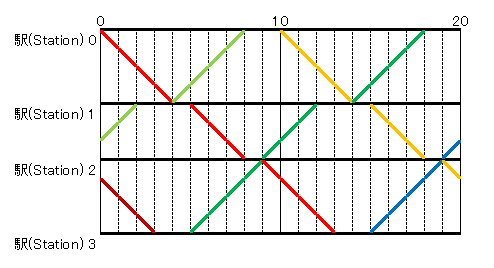
- $1\leq N \leq 100000$ - $1\leq K \leq 10^9$ - $1\leq A_i \leq 10^9$ - $B_i$ 要么是 $1$ 要么是 $2$。 - 所有输入的数都是整数。 ### 部分分 对于 $500$ 分的测试数据，所有铁轨都是单向的，也即 $B_i = 1$。 对于另外 $500$ 分的测试数据，$N \le 200$。 ### 样例解释 1 比如说，在如下的时间表中，答案是 $26$：  在这个时间表中，红线代表的火车在 $0$ 时刻从站台 $0$ 出发，在时刻 $4$ 到达站台 $1$，在 $5$ 时刻从站台 $1$ 出发，在时刻 $8$ 到达站台 $2$，以此类推。