AT_agc011_f [AGC011F] Train Service Planning

[problemUrl]: https://atcoder.jp/contests/agc011/tasks/agc011_f 高橋王国には，$ 1 $ 本の鉄道路線が走っています． この路線は $ N $ 個の区間 $ 1 $, $ 2 $, ..., $ N $ と $ N+1 $ 個の駅 $ 0 $, $ 1 $, ..., $ N $ からなり，区間 $ i $ は駅 $ i-1 $ と駅 $ i $ を直接結んでいます． 列車が区間 $ i $ を走行するには，方向によらず，ちょうど $ A_i $ 分かかります． また，$ N $ 個の区間のそれぞれは，区間全体にわたって複線であるか，区間全体にわたって単線であるかのどちらかです． $ B_i\ =\ 1 $ のときは区間 $ i $ は単線，$ B_i\ =\ 2 $ のときは区間 $ i $ は複線です． 複線の区間では両方向の列車がすれ違うことができますが，単線の区間ではすれ違うことはできません． ただし，列車が駅にいる場合は列車同士がすれ違うことができます． すぬけ君は，この路線に図のように $ K $ 分間隔で列車を走らせようとしています．ここで，太線は列車が走行している位置を表します． (詳しくは，入出力例 1 を見てください．)  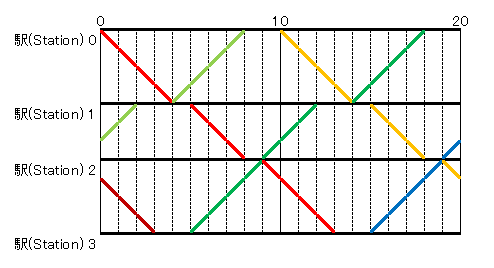このとき，駅 $ 0 $ から駅 $ N $ までの列車の所要時間と，駅 $ N $ から駅 $ 0 $ までの列車の所要時間の合計の最小値を求めてください． この問題の制約の下，適切な列車の走らせ方が存在するとき，この最小値は必ず整数になることが証明できます． なお，列車の発車時刻や到着時刻が満たすべき条件は，厳密に書くと下のようになります． - どの列車も，駅 $ 0 $ を出発して駅 $ N $ まで向かうか，駅 $ N $ を出発して駅 $ 0 $ まで向かうかのいずれかである． - どの列車も，区間 $ i $ をちょうど $ A_i $ 分かけて走行する．例えば，駅 $ N $ 行きのある列車が駅 $ i-1 $ を時刻 $ t $ に出発したなら，この列車は駅 $ i $ にちょうど時刻 $ t+A_i $ に到着する． - ある駅で，時刻 $ s $ に駅 $ N $ 行きの列車が到着し，その列車が時刻 $ t $ に発車したとすると，駅 $ N $ 行きの次の列車は時刻 $ s+K $ に到着し，時刻 $ t+K $ に発車する．また，駅 $ N $ 行きの前の列車は時刻 $ s-K $ に到着し，時刻 $ t-K $ に発車する．駅 $ 0 $ 行きの列車についても同様である． - 異なる方向の列車が，同時に同じ単線区間（両端の駅を除く）を走行していてはならない．

入力は以下の形式で標準入力から与えられる。 > $ N $ $ K $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ : $ A_N $ $ B_N $

駅 $ 0 $ から駅 $ N $ までの列車の所要時間と，駅 $ N $ から駅 $ 0 $ までの列車の所要時間の合計の最小値を表す整数を出力せよ． ただし，条件をすべて満たすように列車を走らせることが不可能な場合は，$ -1 $ を出力せよ．

### 制約 - $ 1\ \leq\ N\ \leq\ 100000 $ - $ 1\ \leq\ K\ \leq\ 10^9 $ - $ 1\ \leq\ A_i\ \leq\ 10^9 $ - $ A_i $ は整数 - $ B_i\ =\ 1 $ または $ B_i\ =\ 2 $ ### 部分点 - $ 500 $ 点分のテストケースでは，すべての区間が単線である．すなわち，$ B_i\ =\ 1 $ が成り立つ． - 別の $ 500 $ 点分のテストケースでは，$ N\ \leq\ 200 $ が成り立つ． ### Sample Explanation 1 例えば，下図に示すように列車を走らせると，所要時間の合計が $ 26 $ 分になります． !\[\](https://atcoder.jp/img/agc011/a5c221ce77ab6ee8aee48e75a4e5c969.png) 例えば，赤線で示した列車は，時刻 $ 0 $ に駅 $ 0 $ を出発し，時刻 $ 4 $ に駅 $ 1 $ に到着し，時刻 $ 5 $ に駅 $ 1 $ を出発し，時刻 $ 8 $ に駅 $ 2 $ に到着します．