AT_agc017_e [AGC017E] Jigsaw
题目描述
有 $N$ 个特殊的拼图块。每个拼图块由三个宽度为 $1$、高度不小于 $1$ 的矩形拼接而成。第 $i$ 个拼图块的构造如下:
- 以高度为 $H$ 的矩形块为中间部分,将高度为 $A_i$ 的矩形块连接在左侧,高度为 $B_i$ 的矩形块连接在右侧。其中,左侧矩形块底边比中间矩形块底边高 $C_i$,右侧矩形块底边比中间矩形块底边高 $D_i$。
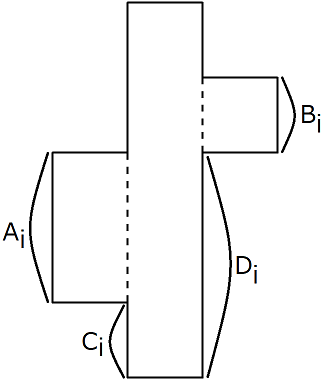
Sune君想把这些拼图块放在一个边长为 $10^{100}$ 的正方形桌子上。此时需要满足以下条件:
- 必须把所有拼图块都放在桌子上。
- 每个拼图块的中间部分底边都要与桌子的前边缘接触。
- 左右两侧的矩形块的底边要么与桌子的前边缘接触,要么与其他某个拼图块的某部分的上边缘完全接触。
- 不能旋转或翻转拼图块。
请判断是否存在一种满足条件的排放方法。
输入格式
输入按以下格式由标准输入给出:
> $N$ $H$ $A_1$ $B_1$ $C_1$ $D_1$ $A_2$ $B_2$ $C_2$ $D_2$ : $A_N$ $B_N$ $C_N$ $D_N$
输出格式
如果存在一种满足条件的拼图块排列方式,输出 `YES`;否则输出 `NO`。
说明/提示
## 范围
- $1\leq N\leq 100000$
- $1\leq H\leq 200$
- $1\leq A_i\leq H$
- $1\leq B_i\leq H$
- $0\leq C_i\leq H-A_i$
- $0\leq D_i\leq H-B_i$
- 所有输入均为整数。
## 样例解释 1
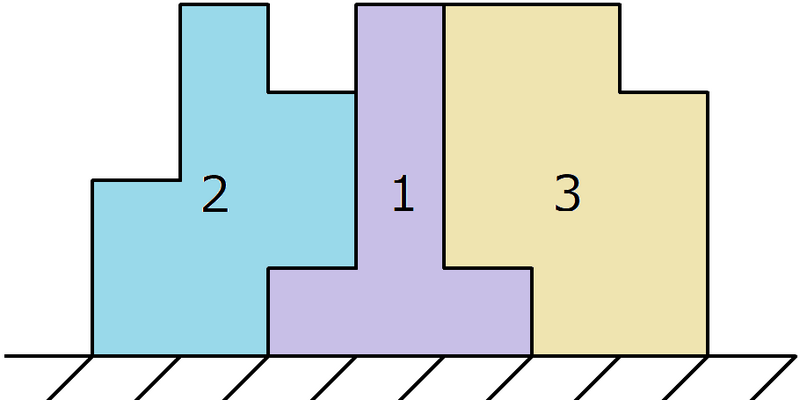
例如,可以按下图方式进行放置。
由 ChatGPT 5 翻译