AT_agc017_f [AGC017F] Zigzag

如上图所示，有 $N$ 个点构成边长为 $1$ 的正三角形，每个点都排列成正三角形的形状，总共有 $N(N+1)/2$ 个点。我们用 $(i,\ j)$ 表示从上往下第 $i$ 行、从左往右第 $j$ 个点（$1\leq i\leq N$，$1\leq j\leq i$）。另外，$(i+1,\ j)$ 是 $(i,\ j)$ 的正左下方的点，$(i+1,\ j+1)$ 是 $(i,\ j)$ 的正右下方的点。 高桥君打算在这些点之间画 $M$ 条折线 $1,2,\ldots, M$。每条折线都从 $(1,1)$ 出发，随后「每次选择当前位置的正左下方或正右下方的点，用直线连接到那个点并移动过去」，重复 $N-1$ 次。因此，存在某些 $X_{i,1},\ldots, X_{i,N}$ 满足以下条件： - 折线 $i$ 依次连接 $N$ 个点 $(1,\ X_{i,1}),\ (2,\ X_{i,2}),\ldots,(N,\ X_{i,N})$。 - 对于 $j=1,2,\ldots, N-1$，有 $X_{i,j+1} = X_{i,j}$ 或 $X_{i,j+1}=X_{i,j}+1$。 高桥君希望画图时，编号大的折线不会位于编号小的折线左边。也就是说，对于 $j=1,2,\ldots,N$，有 $X_{1,j}\leq X_{2,j}\leq\ldots\leq X_{M,j}$。 此外，高桥君还需要满足关于曲线拐弯的 $K$ 个条件。第 $i$ 个条件 $(A_i,\ B_i,\ C_i)$ 的意义如下： - 当 $C_i=0$ 时，画折线 $A_i$ 时，在第 $B_i$ 次移动时，必须选择左下方的点。 - 当 $C_i=1$ 时，画折线 $A_i$ 时，在第 $B_i$ 次移动时，必须选择右下方的点。 换句话说，$X_{A_i,B_i+1} = X_{A_i,B_i} + C_i$。 请计算，高桥君能画出不同的 $M$ 条折线的方案数，对 $1000000007$ 取模后输出。

输入从标准输入读入，格式如下： > $N$ $M$ $K$ $A_1$ $B_1$ $C_1$ $A_2$ $B_2$ $C_2$ $\ldots$ $A_K$ $B_K$ $C_K$

输出高桥君画 $M$ 条折线的方案数，对 $1000000007$ 取模。

### 注意 提交前，强烈建议使用“代码测试”测量运行时间。 ### 限制 - $1\leq N\leq 20$ - $1\leq M\leq 20$ - $0\leq K\leq (N-1)M$ - $1\leq A_i\leq M$ - $1\leq B_i\leq N-1$ - $C_i=0,1$ - $(A_i,B_i)$ 作为同一组不会重复出现多次。 ### 样例解释 1 如图所示，共有 $6$ 种画法。红线表示折线 $1$，绿色表示折线 $2$。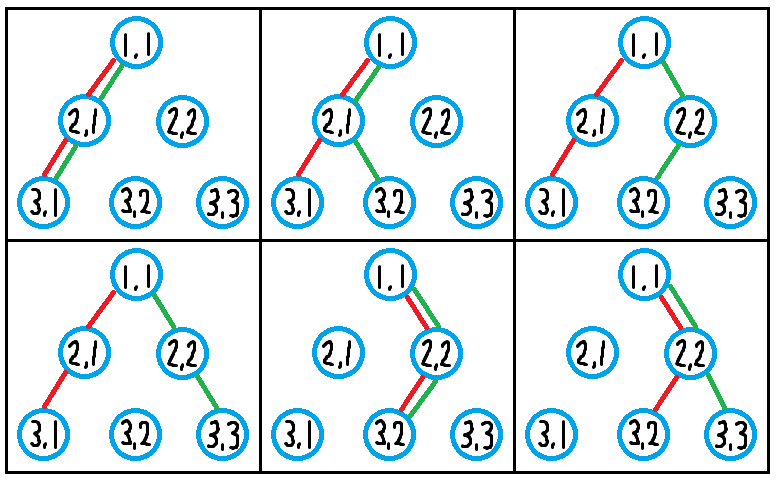 由 ChatGPT 5 翻译