AT_agc039_e [AGC039E] Pairing Points

在圆周上一般位置上有 $2N$ 个不同的点，按逆时针顺序依次编号为 $1,\dots,2N$。这里所说的“一般位置”是指，对于任意互不相同的 $6$ 个点 $U,V,W,X,Y,Z$，线段 $UV, WX, YZ$ 不会交于同一点。此外，给定一个 $2N \times 2N$ 的矩阵 $A$。 请计算将圆周上的 $2N$ 个点分成 $N$ 个配对的方法数，要求满足以下条件： - 对于所有的配对，将每对点用红色线段连接后，所有红色部分构成一棵“树”。 - 对于每一对配对的端点 $P, Q$，有 $A_{P,Q} = A_{Q,P} = 1$。 更严格地说，红色部分构成“树”是指红色部分整体连通且无环。 例如，下图中： - 左上角的例子满足条件。 - 右上角的例子中，红色部分存在环，不满足条件。 - 左下角的例子中，红色部分不连通，不满足条件。 - 右下角的例子中，存在未被配对的顶点或某些顶点被多次配对，不满足条件。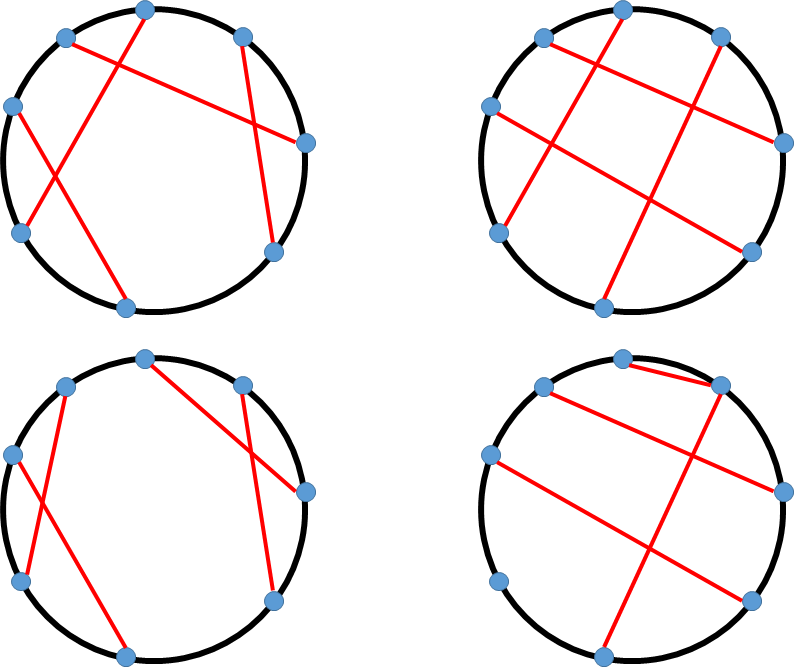  图：满足条件的例子（左上）和不满足条件的例子（其他）

输入按以下格式从标准输入读入。 > $N$ > $A_{1,1}\ A_{1,2}\ \dots\ A_{1,2N}$ > $A_{2,1}\ A_{2,2}\ \dots\ A_{2,2N}$ > $\vdots$ > $A_{2N,1}\ A_{2N,2}\ \dots\ A_{2N,2N}$

输出将圆周上的 $2N$ 个点分成 $N$ 个配对且满足条件的方法数。在本题限制下，可以证明答案不会超过 $64$ 位有符号整数的范围。

### 说明 可以证明，只要 $2N$ 个点处于一般位置，答案与这些点的具体位置关系无关。 ### 限制 - $1 \leq N \leq 20$ - $A_{i,j}$ 为 `0` 或 `1` - $A_{i,i}$ 为 `0` - $A_{i,j} = A_{j,i}$ - $N$ 为整数 ### 样例解释 1 $((1,4),(2,6),(3,5))$，$((1,3),(2,5),(4,6))$，$((1,5),(2,4),(3,6))$ 这三种分组方式满足条件。 由 ChatGPT 4.1 翻译