AT_agc047_d [AGC047D] Twin Binary Trees

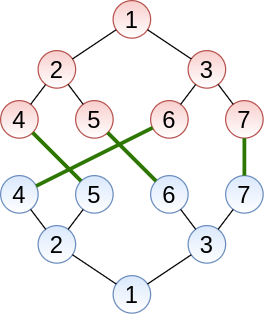
受到电视剧《怪奇物语》的启发，熊的 Rimac 决定在现实世界和镜像世界之间来回穿梭。 有两棵高度为 $H$ 的完全二叉树，每个顶点按照标准方式编号，从 $1$ 到 $2^H-1$。也就是说，根节点编号为 $1$，编号为 $x$ 的节点的子节点编号分别为 $2 \cdot x$ 和 $2 \cdot x + 1$。 设一棵树的叶子数为 $L$，即 $L = 2^{H-1}$。 给定 $1, \ldots, L$ 的一个排列 $P_1, P_2, \ldots, P_L$。这表示两棵树之间有 $L$ 条*特殊边*。即，第一棵树中编号为 $L+i-1$ 的顶点与第二棵树中编号为 $L+P_i-1$ 的顶点通过一条特殊边相连。  *输入样例 1 的图示。$P = (2, 3, 1, 4)$，绿色的边为特殊边* 定义一个环的*积*为其包含的所有顶点编号的乘积。请你求出**恰好包含两条特殊边的**所有简单环的积之和，并对 $10^9+7$ 取模。 这里，简单环指的是长度不少于 $3$，且没有重复顶点和边的环。

输入以如下格式从标准输入读入（其中 $L = 2^{H-1}$）： > $H$ $P_1$ $P_2$ $\cdots$ $P_L$

请输出恰好包含两条特殊边的所有简单环的积之和，并对 $10^9+7$ 取模。

### 限制 - $2 \leq H \leq 18$ - $1 \leq P_i \leq L$（其中 $L = 2^{H-1}$） - $P_i \neq P_j$（即该数列是 $1, \ldots, L$ 的一个排列） ### 样例解释 1 下图展示了需要考虑的两个环（实际上还有其他）。第一个环的积为 $2 \cdot 5 \cdot 6 \cdot 3 \cdot 1 \cdot 2 \cdot 5 \cdot 4 = 7200$，第二个环的积为 $1 \cdot 3 \cdot 7 \cdot 7 \cdot 3 \cdot 1 \cdot 2 \cdot 5 \cdot 4 \cdot 2 = 35280$。第三个环不满足恰好有两条特殊边，因此不计入答案。  ### 样例解释 2 图中唯一的环确实包含两条特殊边，其顶点编号的积为 $1 \cdot 3 \cdot 3 \cdot 1 \cdot 2 \cdot 2 = 36$。 由 ChatGPT 4.1 翻译