AT_agc047_d [AGC047D] Twin Binary Trees

[problemUrl]: https://atcoder.jp/contests/agc047/tasks/agc047_d テレビドラマシリーズ『ストレンジャー・シングス』に触発されたクマのリマクは、現実世界と鏡像世界を歩いて行き来することにしました。 二つの高さ $ H $ の完全二分木があり、それぞれの頂点は $ 1 $ から $ 2^H-1 $ までの標準的な番号付けがなされています。 すなわち、根の番号は $ 1 $ で、番号 $ x $ の子の番号は $ 2\ \cdot\ x $ と $ 2\ \cdot\ x\ +\ 1 $ です。 一つの木が持つ葉の数を $ L $ とします。すなわち、$ L\ =\ 2^{H-1} $ です。 数列 $ 1,\ \ldots,\ L $ の順列 $ P_1,\ P_2,\ \ldots,\ P_L $ が与えられます。これは、二つの木を結ぶ $ L $ 本の *特殊辺* を表します。 すなわち、第一の木の番号 $ L+i-1 $ の頂点と第二の木の番号 $ L+P_i-1 $ の頂点が一本の特殊辺で結ばれています。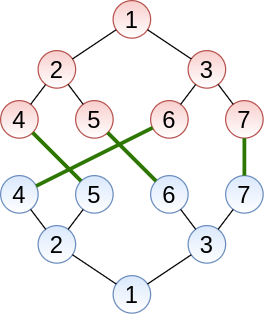  *入力例 1 の図示。$ P\ =\ (2,\ 3,\ 1,\ 4) $ であり、緑の辺が特殊辺* サイクルの *積* を、それに含まれる頂点の番号の積と定義します。**ちょうど二本の特殊辺を持つような** すべての単純サイクルの積の和を $ (10^9+7) $ で割った余りを求めてください。 なお、単純サイクルとは、長さが $ 3 $ 以上であって頂点や辺の重複がないようなサイクルです。

入力は以下の形式で標準入力から与えられる (ここで、$ L\ =\ 2^{H-1} $ である)。 > $ H $ $ P_1 $ $ P_2 $ $ \cdots $ $ P_L $

ちょうど二本の特殊辺を持つようなすべての単純サイクルの積の和を求め、それを $ (10^9+7) $ で割った余りを出力せよ。

### 制約 - $ 2\ \leq\ H\ \leq\ 18 $ - $ 1\ \leq\ P_i\ \leq\ L $ (ただし $ L\ =\ 2^{H-1} $) - $ P_i\ \neq\ P_j $ (すなわち、この数列は $ 1,\ \ldots,\ L $ の順列である) ### Sample Explanation 1 下図に考慮すべきサイクルを二つ示します (他にも存在します)。一つめのサイクルの積は $ 2\ \cdot\ 5\ \cdot\ 6\ \cdot\ 3\ \cdot\ 1\ \cdot\ 2\ \cdot\ 5\ \cdot\ 4\ =\ 7200 $、二つめのサイクルの積は $ 1\ \cdot\ 3\ \cdot\ 7\ \cdot\ 7\ \cdot\ 3\ \cdot\ 1\ \cdot\ 2\ \cdot\ 5\ \cdot\ 4\ \cdot\ 2\ =\ 35280 $ です。三つめのサイクルは、特殊辺の数が二本でないため、考慮すべきサイクルではありません。 !\[three cycles\](https://img.atcoder.jp/agc047/3\_trees\_font.png) ### Sample Explanation 2 グラフ中の唯一のサイクルは確かに特殊辺を二本持ち、その頂点番号の積は $ 1\ \cdot\ 3\ \cdot\ 3\ \cdot\ 1\ \cdot\ 2\ \cdot\ 2\ =\ 36 $ です。